1. Cel ćwiczenia

Celem ćwiczenia jest prezentacja metody diagnostycznej SFRA (ang. Sweep Frequency Response Analysis) dla transformatorów. W ramach ćwiczenia należy przeanalizować wyniki pomiarów wykonanych na fizycznym modelu transformatora elektroenergetycznego oraz wykonanie aproksymacji przebiegów za pomocą metody vector fitting.

2. Podstawy teoretyczne

Podstawą diagnostyki i badań naukowych jest pomiar. Zgodnie z definicją encyklopedyczną [1], pomiar rozumiany jest jako zbiór określonych działań i doświadczeń, za pomocą których wyznaczana jest wartość mierzonej wielkości. Poza przygotowaniem teoretycznym i praktycznym oraz realizacją techniczną, pojęcie obejmuje także interpretację wyników. Pomiary charakterystyk częstotliwościowych wiążą się ściśle z użyciem specjalistycznego sprzętu pomiarowego oraz komputera. Każdy pomiar jest obciążony pewnymi błędami, wynikającymi z różnych przyczyn, np. wpływem czynników zewnętrznych na przyrząd pomiarowy, błędy obsługi, itp.
Każda usterka transformatora powoduje straty finansowe dla spółki energetycznej. Może także powodować przerwy w dostawie energii, przymusowe odstawienie urządzenia oraz jego naprawę. Odstawienie urządzenia z uwagi na jego awarię powinno być odnotowane ze szczególnym uwzględnieniem czasu wystąpienia usterki, przyczyn, danych znamionowych urządzenia. Ma to na celu zbudowanie bazy danych, która może być pomocna w przypadku wystąpienia kolejnych awarii lub przy podejmowaniu decyzji odnośnie przyszłej eksploatacji.
Każde odstawienie jednostki stwarza problemy natury technicznej, ponieważ aby ponownie jednostkę uruchomić trzeba znaleźć przyczynę usterki, usunąć ją i zabezpieczyć przed ponownym powstaniem wady. W. H. Bartley w swojej publikacji przedstawił 11 podstawowych przyczyn powstawania uszkodzeń transformatorów:
– Usterki izolacji – główna i zarazem najdroższa przyczyna. Istnieją 4 podstawowe czynniki wpływające na pogorszenie stanu izolacji: ciepło, utlenianie, kwasowość i wilgoć.
– Usterki podczas procesu projektowania i związane z fizycznym wykonaniem urządzenia
– Zanieczyszczenia oleju dla transformatorów olejowych
– Przeciążenia (długotrwałe, związane z niekorzystnymi efektami termicznymi)
– Pożar lub eksplozja – traktowane jako czynnik zewnętrzny nie wynikający z wewnętrznych usterek, mogących powodować pożar lub eksplozję transformatora
– Przepięcia łączeniowe
– Usterki eksploatacyjne i konserwacyjne
– Powódź
– Niewłaściwie wykonane połączenia
– Wyładowanie atmosferyczne
– Wilgoć.

3. Model fizyczny transformatora

Założenia modelu opierały się na wykorzystaniu transformatora suchego typu TRIHAL o mocy 250 kVA i przekładni 15/0,4 kV (dane znamionowe pokazano w tabeli 1). Rdzeń transformatora został rozpakietowany w celu usunięcia uzwojeń wysokiego napięcia (które okazały się być po prostu atrapą – transformator służył do celów pokazowych).

Tabela 1. Dane znamionowe transformatora

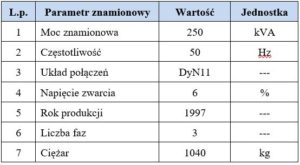
Na rysunku 1 pokazano rozpakietowany transformator testowy. Rdzeń został zdemontowany tylko w zakresie jarzma górnego. Dzięki temu było można z poszczególnych kolumn zdjąć uzwojenia wysokiego napięcia i zamontować nowe uzwojenia dla celów badań. Uzwojenia niskiego napięcia transformatora pozostawiono – są zbudowane z blachy aluminiowej. Transformator po zainstalowaniu nowych uzwojeń testowych zostanie ponownie złożony i obwód magnetyczny będzie zamknięty.

Rys. 1. Transformator testowy typu TRIHAL w trakcie rozpakietowywania rdzenia

W celu budowy modelu fizycznego wykonano cewki z taśmy miedzianej o szerokości 20 mm i grubości 1 mm. Każda cewka miała po 30 zwojów, a każdy zwój został zaizolowany za pomocą taśmy izolacyjnej.
Dla określenia warunków pomiaru zostały wykonane testy układu. Badano wpływ obecności ekranu na pomiar (dla wyrównania pola elektromagnetycznego wewnątrz cewek) oraz wpływ sposobu przyłączenia ekranu do cewki (odczepy uzwojenia cewki były wewnątrz i na zewnątrz cewki). Układ pomiarowy pokazano na rysunku 2.

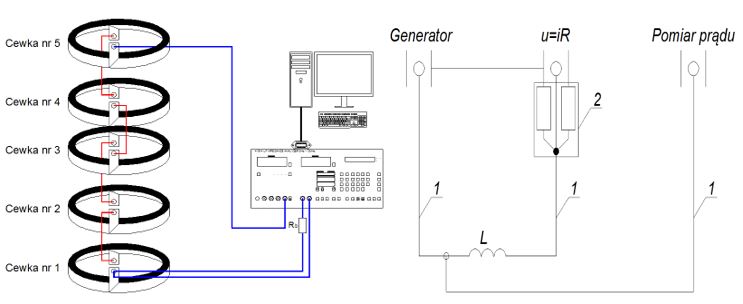
Rys. 2. Schemat układu pomiarowego do weryfikacji zbudowanych cewek: 1 – kable pomiarowe; 2 – bocznik pomiarowy

Analizator impedancji HP4196A mierzył charakterystykę częstotliwościową cewki wzorcowej w określonym zakresie 10 – 107 Hz – skala logarytmiczna (1):

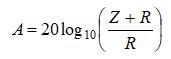
(1)

 

gdzie: Z – impedancja cewki wzorcowej, R – rezystancja bocznika pomiarowego.

4. Metoda SFRA

Metoda odpowiedzi częstotliwościowej (ang. Frequency Response Analysis – FRA) powstała w 1978 r. [2]. Standardowa FRA bazuje na graficznej interpretacji pomiaru impedancji uzwojeń transformatora w szerokim spektrum częstotliwości. Funkcja wymierna, opisująca określony przebieg impedancyjny, jest porównywana z funkcją referencyjną, tj. zdjętą np. z tego samego transformatora w momencie instalacji lub z jednostki identycznej (tzw. odcisk palca – ang. fingerprint). Zmiany w kształcie funkcji i częstotliwościach rezonansowych są głównymi wskaźnikami odpowiednich zmian uzwojenia lub rdzenia. Zgodnie z [3], za pomocą metody FRA można wykryć następujące usterki:
– Zwarcia zwojowe i w przewodach równoległych
– Uszkodzenia i nieprawidłowości w obwodzie magnetycznym (uziemienie rdzenia, ekranów, itp.)
– Niesprężyste deformacje geometryczne uzwojeń (osiowe i promieniowe)
– Przesunięcie uzwojeń na kolumnach rdzenia
– Uszkodzenia izolatorów przepustowych
– Uszkodzenia w obrębie przełącznika zaczepów pod obciążeniem
– Uszkodzenia mechaniczne powstałe wskutek transportu transformatora.
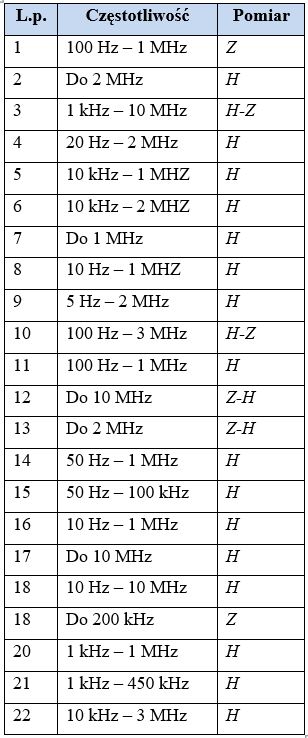
Odpowiedź częstotliwościową można otrzymać za pomocą dwóch metod pomiarowych: LVI i SFRA (ang. Sweep Frequency Response Analysis). Pomiar metodą SFRA polega na przyłożeniu do uzwojeń transformatora sygnału sinusoidalnego o częstotliwości zmienianej w szerokim zakresie i rejestracji odpowiedzi urządzenia w funkcji częstotliwości. Zakres częstotliwości sygnału wymuszającego został podany w tabeli 2 [4], gdzie w trzeciej kolumnie oznaczono, czy pomiar dotyczył impedancji (Z), transmitancji (H) opisanych poniższymi wzorami (1). Skok częstotliwości należy dobrać w ten sposób, aby był poniżej 2% wartości poprzedniej częstotliwości.

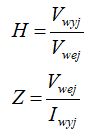
(2)

 

 

 

Tabela 2. Zakresy pomiarowe częstotliwości sygnału wymuszającego [4]

Pomiary wykonuje się w dwóch układach przedstawionych na rysunku 3, przy czym obydwa układy mogą mierzyć zarówno impedancję jak i transmitancję.

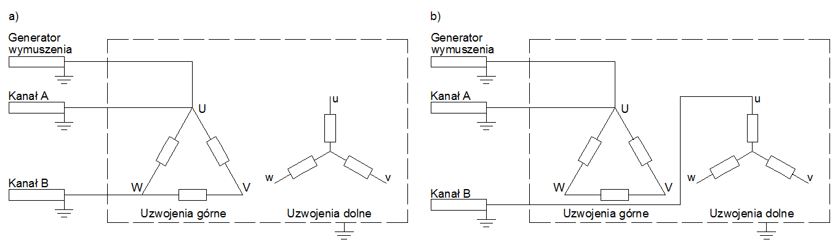
Rys. 3. Schemat blokowy układu pomiarowego techniką SFRA [4]: a) zaciski pomiarowe wpięte w obwód tej samej strony napięcia b) zaciski pomiarowe wpięte w obwody o różnych stronach napięcia

Warto zwrócić uwagę, iż pomiar wykonany metodą SFRA na jednostce uszkodzonej może jedynie potwierdzić wystąpienie uszkodzenia wraz z ujawnieniem jego skali i lokalizacji. Diagnostyka SFRA ma istotne znaczenie przy prowadzeniu diagnostyki okresowej, kiedy możliwe jest śledzenie stanu technicznego transformatora. Ma to zastosowanie w odpowiednio wczesnym formułowaniu zaleceń i wniosków odnośnie dalszej eksploatacji, przy planowaniu procesów remontowych itp., co wiąże się z polepszeniem niezawodności systemu elektroenergetycznego.
Badanie metodą SFRA jest relatywnie dłuższe niż w przypadku LVI. Dodatkowo, powstaje problem odnośnie interpretacji wyników. Zakłada się więc dwa podejścia [4]:
a) Analiza porównawcza wyników, przy założeniu posiadania pomiarów na nieuszkodzonej, tej samej jednostce.
b) Analiza porównawcza wyników przy użyciu pomiarów:
– wykonanych na różnych fazach tego samego transformatora
– wykonanych na jednostce „bliźniaczej”.

Samej analizie podlegają zmiany w kształcie otrzymanych krzywych w dziedzinie częstotliwości, pojawienie się nowych punktów rezonansowych lub zanik rezonansów występujących przy jednostce sprawnej oraz znaczne przesunięcia w częstotliwościach rezonansowych. W celu ilościowego określenia różnic w pomiarach zostały zdefiniowane parametry:
– Współczynnik korelacji (ang. Correlation Coefficient – CC) definiowany poniższym równaniem

 

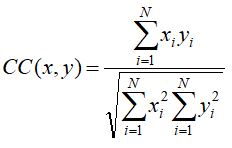
(3)

 

 

 

 

 

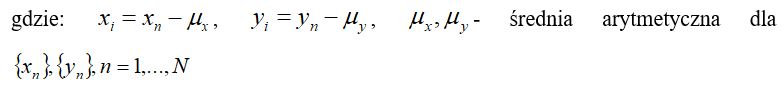
– Odchylenie standardowe (ang. Standard Deviation – SD)
– Maksymalna bezwzględna różnica (ang. Maximum Absolute Difference – DABS) definiowana poniższym równaniem

 

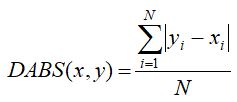
(4)

 

 

 

– Błąd sumy kwadratów (ang. Sum of Squares Error – SSE)
– Współczynnik błędu sumy kwadratów (ang. Sum Squared Ratio Error – SSRE)
– Błąd max-min sumy kwadratów (ang. Sum Square Max-Min Error – SSMMRE)
– Błąd bezwzględnej sumy logarytmów (ang. Absolute Sum of Logarythmic Error – ASLE) definiowany poniższym równaniem

 

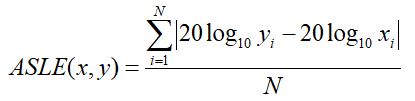
(5)

 

 

 

Z rozważań i badań nad powyższymi parametrami wynika, iż CC jest użyteczny statystycznie, natomiast SD jest parametrem mało wiarygodnym porównawczo. Współczynnik CC jest mało wrażliwy na detekcję zmian w odpowiedzi częstotliwościowej podobnych krzywych ze stałą różnicą w amplitudzie. W zasadzie większość z powyższych parametrów, poza ASLE, posiada niepożądane wady numeryczne, jednak dla wszystkich nadal brakuje wyznaczonego normalnego zakresu zmienności [5].
W związku z powyższymi trudnościami zostały zaproponowane inne sposoby, w celu zapewnienia skutecznej interpretacji wyników pomiarów. Poniżej w tabeli 3 określono je, wraz z ich zaletami i wadami.

Tabela 3. Propozycje skutecznej interpretacji wyników pomiarów metodą SFRA

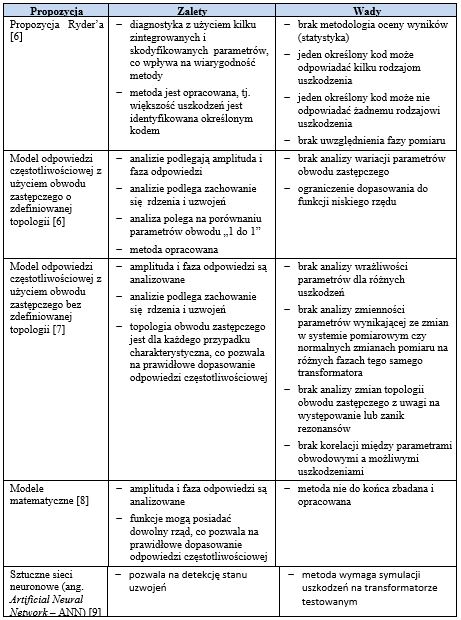
Jak widać z tabeli 3, istnieje kilka sposobów do interpretacji wyników pomiarów metodą SFRA, jednak należy zauważyć, iż w praktyce istnieje wiele źródeł niepewności i niedokładności wyników pomiarów. Odpowiedzią częstotliwościową układu liniowego na wymuszenie sinusoidalne o zmiennej częstotliwości jest także sinusoida z różną amplitudą i fazą. Wymusza to wzięcie pod uwagę podczas analizy metody dwóch czynników [4]:

• – Należy jedynie używać takiego zakresu częstotliwości, w którym przewiduje się liniowość systemu mierzonego
• – Należy brać pod uwagę amplitudę i fazę pomiaru.

Pierwszy z powyższych czynników ma związek z efektem występowania rdzenia magnetycznego. Zakłada się, że wraz ze wzrostem częstotliwości sygnału oddziałującego na rdzeń transformatora, głębokość wnikania pola magnetycznego się zmniejsza. Warto odnotować, iż badania dotyczące powyższego wpływu rdzenia transformatora na charakterystyki częstotliwościowe są nadal wykonywane.

Metoda FRA jest nadal rozwijana i badana, szczególnie na potrzeby interpretacji jej wyników. Modelowanie jest skuteczną i dużo tańszą metodą od badań empirycznych. W tym przypadku stanowi pewien opis matematyczny urządzenia. Opis matematyczny najłatwiej w tym przypadku określić przy pomocy rachunku operatorowego, który jest pewnym sposobem rozwiązywania niektórych równań i układów równań różniczkowych oraz pokrewnych, za pomocą algebraizacji rozwiązywanego równania lub układu równań i przy użyciu zmiennej operatorowej Laplace’a s. Model matematyczny opisujący funkcję obwodową charakterystyki częstotliwościowej transformatora jest równaniem liniowym ze stałymi współczynnikami, a więc można do jego rozwiązania zastosować rachunek operatorowy. Algebraizacja równań polega na wyznaczeniu z równań np. różniczkowych równania algebraicznego, czyli zamianie operacji różniczkowania przez np. mnożenie. Proces ten może być zrealizowany np. za pomocą przekształcenia Laplace’a, określonego wzorem:

 

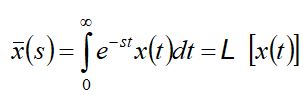
(6)

 

Znając równanie operatorowe można następnie wyznaczyć funkcje x(t):

 

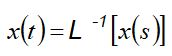
(7)

Funkcja operatorowa H(s) może być ogólnie zdefiniowana jako reprezentacja matematyczna ilorazu sygnału wejściowego i wyjściowego dla systemu liniowego niezależnego od czasu, z zerowymi warunkami początkowymi:

 

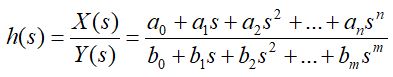
(8)

 

Funkcję (8) można różnie interpretować w zależności od sygnałów wejściowych i wyjściowych, np. dla sygnałów napięciowego i prądowego otrzymuje się funkcję operatorową impedancji (Rys. 4).

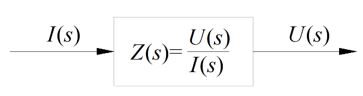
Rys. 4. Schemat blokowy funkcji operatorowej impedancji

Funkcja operatorowa w tym przypadku (Rys. 4) reprezentuje zarówno amplitudę jak i fazę odpowiedzi częstotliwościowej takiego systemu.

5.    Zadanie

Na podstawie przekazanych danych pomiarowych amplitudy i fazy należy:

• Dokonać przeglądu literatur pod kątem metody SFRA (min. 5 pozycji – artykułów) wraz z opisem w raporcie.
• Wyznaczyć charakterystykę częstotliwościową impedancji zmierzonego sygnału.

SKOS0 POM1CM0 POMDP0 POM0CM0 POM2CM0 – pliki z danymi pomiarowymi

cewind2 – plik ze skryptem do programu Matlab

• Porównać zmierzone przebiegi i określić odchylenia od standardowego ustawienia cewek.
• Znaleźć, za pomocą funkcji rationalfit, aproksymację zadanego przebiegu. Wyznaczyć dla każdego funkcję H(s).
• Na podstawie aproksymacji określić zmiany w pomiarach.
• Na podstawie powyższych danych wykonać raport.

6. Pytania testowe

1. Czym jest transformator i jakie funkcje pełni w elektroenergetyce?
2. Wymień i krótko opisz podstawowe usterki transformatorów elektroenergetycznych?
3. Opisz, na czym polega pomiar odpowiedzi częstotliwościowej transformatorów.
4. Jakie uszkodzenia można diagnozować metodą SFRA?
5. Do czego potrzebna jest funkcja operatorowa powstała z aproksymacji charakterystyk częstotliwościowych?

7.    Literatura

1. Bąk, J. Bek, L. Bukowski, i inni, „Mała encyklopedia metrologii”, WNT, Warszawa 1989
2. P. Dick, C. C. Ereven, “Transformer diagnostic by frequency response analysis”, IEEE Trans. On Power Apparatus and Systems, Vol. PAS-97, No. 6, Nov/Dec 1978
3. “Guide for transformer maintenance”, CIGRE 445, Working Group A2.34, Luty 2011
4. R. Secue, E.Mombello, “Sweep frequency response analysis (SFRA) for the assessment of winding displacements and deformation in power transformers”, Electric Power Systems Research 78 (2008) 1119-1128, Wrzesień 2007
5. Semlyen, “Contributions to the Theory of Electromagnetic Transients on Transmission Lines with Frequency Dependent Parameters”, IEEE PES Summer Meeting, Vancouver, B.C. July 1979
6. A. Ryder, “A new method for diagnosing transformer faults using frequency response analysis”, Cigre SC A2, Czerwiec 2003 Merida, Meksyk, Colloquium
7. Pleite, E. Olias, A. Barrado, A. Lazaro, J.Vazquez, “Transformer modeling for FRA techniques in: Transmission and Distribution”, Conference and Exhibition 2002: Asia Pacific. IEEE/PES, vol. 1, 6–10 October, 2002, pp. 317–321
8. Akcay, S.M. Islam, B. Ninness, “Subspace-based identification of power transformer models from frequency response data”, Instrum. Measur. IEEE Trans. 48 (3) (1999) 700–704
9. J. Zhijian, L. Jingtao, Z. Zishu, “Diagnosis of transformer winding deformation on the basis of artificial neural network”, Proceedings of the 6th International Conference on Properties and Applications of Dielectric Materials, vol. 1, 21–26 June, 2000, pp. 173–176