1. Cel ćwiczenia
Celem ćwiczenia jest zaprojektowanie przyrządu pomiarowego – dzielnika napięcia na podstawie rzeczywistych elementów i ich rzeczywistych parametrów znamionowych. Wynikiem prac projektowych będzie raport techniczny.
2. Podstawy teoretyczne
Zadaniem napięciowego dzielnika pomiarowego jest obniżenie wartości mierzonego napięcia do wartości napięcia dostosowanej do zakresu przyrządu pomiarowego. Przekładnia dzielnika to iloraz napięcia doprowadzonego do dzielnika do napięcia na jego wyjściu. Teoretycznie przy dzielniku wykonanym z identycznych elementów, o jednakowej impedancji, wyznaczenie przekładni nie stanowi żadnego problemu. W takim przypadku przekładnia zależy tylko od liczby elementów dzielnika. Problem z wyznaczeniem przekładni dzielnika na podstawie jego impedancji wzrasta wraz ze wzrostem wartości napięcia wejściowego U1, jak również jego zmian w czasie du/dt. Dla wysokich wartości napięcia i wraz ze wzrostem częstotliwości znaczną rolę zaczynają odgrywać pojemności występujące w układzie dzielnika związane z połączeniami jego elementów, jak i pojemnością występującą pomiędzy elementami dzielnika, a ziemią.
Dzielnik napięcia, pokazany schematycznie na rys. 1, można opisać równaniami (1).
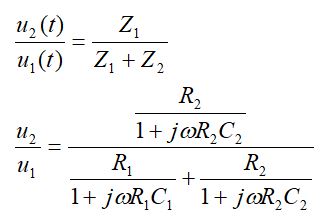
(1)
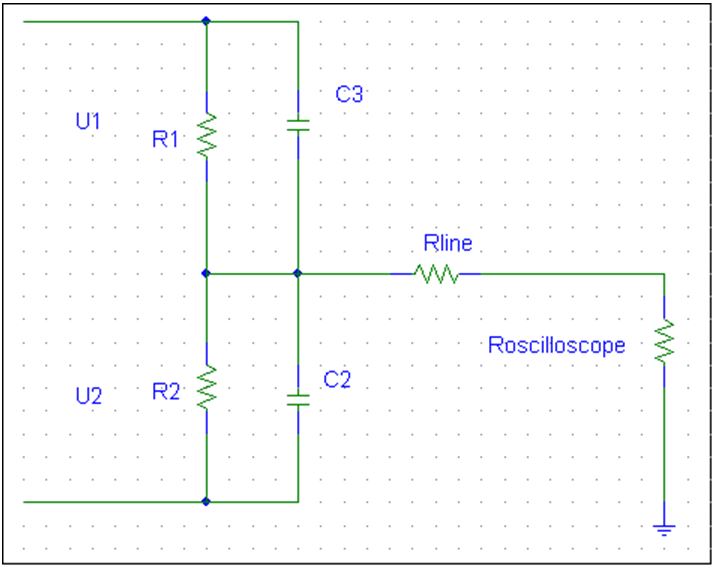
Rys. 1. Schemat obwodowy dzielnika napięcia
W technice wysokonapięciowej do pomiarów napięcia wykorzystywane są dzielniki rezystancyjne, pojemnościowe i rezystancyjno-pojemnościowe. Dzielniki rezystancyjne nadają się do pomiaru napięć stałych, przemiennych i udarowych. Dzielniki pojemnościowe wykorzystywane są do pomiaru napięć udarowych i przemiennych.
Na rys. 2 pokazano schemat zastępczy dzielnika uwzględniający impedancję. Na rysunku 2 oznaczono odpowiednio pojemność doziemną poszczególnych członów dzielnika jako C’z, C’s to pojemność międzyelmentowa elementów dzielnika, a Z’s to impedancja członu dzielnika o parametrach rezystancji R’, indukcyjności L’ i pojemności C’.
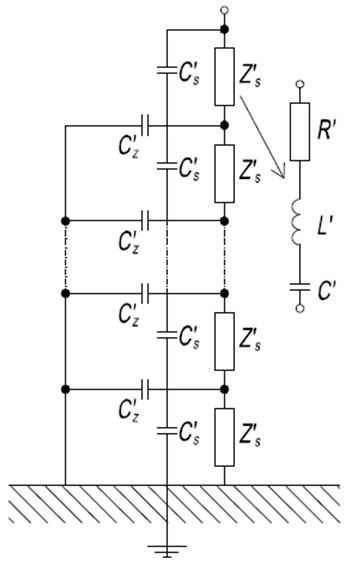
Rys. 2. Schemat zastępczy dzielnika uwzględniający impedancję
W dzielnikach rezystancyjnych można w znacznym stopniu zniwelować wpływ indukcyjności poprzez odpowiednie wykonanie rezystorów składających się na kolumnę dzielnika. Ponadto na dokładność podziału dzielnika indukcyjność ma znacznie mniejszy wpływ niż pojemności. Pojemności międzyelmentowe są wielokrotnie mniejsze od pojemności doziemnych. Fakt ten w pewnym uproszczeniu pozwala na pominięcie pojemności międzyelmentowych. Znacznie uproszczą się wówczas obliczenia związane z wyznaczeniem czasu odpowiedzi dzielnika na sygnał wejściowy. Aby wyeliminować wpływ pojemności w poszczególnych członach dzielnika na jego dokładność podziału napięcia niezależnie od częstotliwości możliwym rozwiązaniem jest skompensowanie dzielnika. Dzielnik wykonany z elementów o takiej samej impedancji będzie dzielnikiem skompensowanym. W takim dzielniku przesunięcia fazowe pomiędzy prądem i napięciem na każdym z członów dzielnika będą identyczne. Uproszczony schemat układu skompensowanego częstotliwościowo dzielnika przedstawia rysunek 3. W tym przypadku dzielnik ma charakter mieszany, rezystancyjno-pojemnościowy.
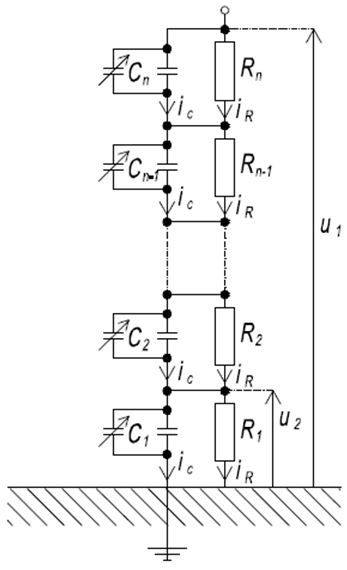
Rys. 3. Schemat skompensowanego częstotliwościowo dzielnika rezystancyjnego
Pojemności oznaczone na rysunku 3, C1 do Cn to pojemności poszczególnych członów dzielnika, na schemacie przedstawione jako równoległe połączenie kondensatora stałego, reprezentującego pojemność własną członu dzielnika i kondensatora nastawnego, jako elementu kompensacyjnego. Rezystancje członów dzielnika oznaczono jako R1 do Rn. Prąd ic jest prądem płynącym przez pojemności poszczególnych członów dzielnika. Prąd iR jest prądem płynącym przez rezystancję. W dzielniku skompensowanym, w każdym z członów płyną prądy pojemnościowe i rezystancyjne o takich samych wartościach. Odpowiednio napięcie na wejściu i na wyjściu dzielnika oznaczono jako u1 i u2. Przy założeniu, że przez pojemności będzie płyną taki sam prąd, pojemność poszczególnych członów dzielnika nie wpłynie na jego dokładność podziału napięcia. Rezystancja w członach dzielnika będzie skompensowana, gdy stałe czasowe tych członów będą sobie równe. Czyli będzie spełniona zależność opisane poniższymi wzorami (2).
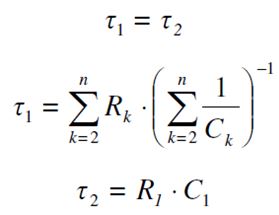
(2)
Dzielnik jest układem liniowy opisanym transmitancją. Należy zaznaczyć, że w rzeczywistych warunkach dzielnik pracuje w pewnym układzie pomiarowym i w praktyce nie można go rozpatrywać samodzielnie. Rozważmy teoretyczny układ dzielnika składający się z kolumny n rezystorów o jednakowej wartości rezystancji. Układ dzielnika składający się z dwóch połączonych członów, inercyjnego pierwszego rzędu o transmitancji G1 i proporcjonalnego o transmitancji G2, przedstawia rysunek 4.
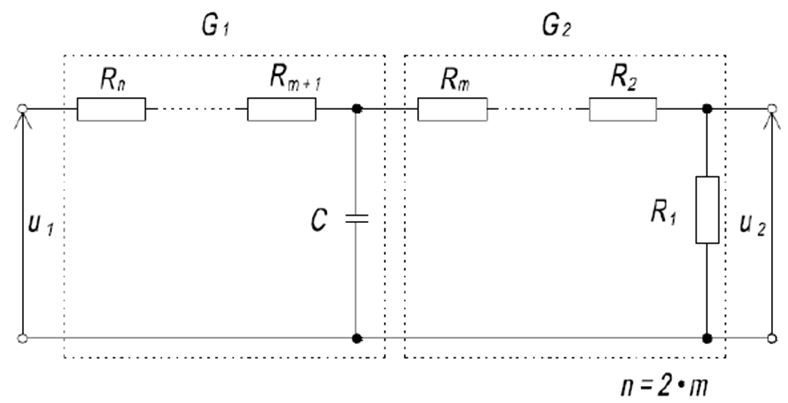
Rys. 4. Schemat układu kolumny dzielnika
Funkcja operatorowa H(s) może być ogólnie zdefiniowana jako reprezentacja matematyczna ilorazu sygnału wejściowego i wyjściowego dla systemu liniowego niezależnego od czasu, z zerowymi warunkami początkowymi (3).
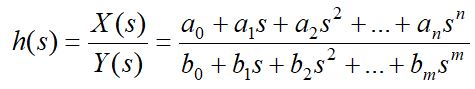
(3)
Funkcję powyższą można różnie interpretować w zależności od sygnałów wejściowych i wyjściowych, np. dla sygnałów napięciowego i prądowego otrzymuje się funkcję operatorową impedancji (Rys. 5).
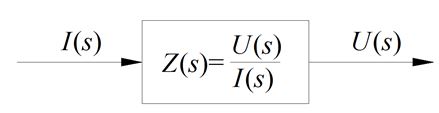
Rys. 5. Schemat blokowy funkcji operatorowej impedancji
Funkcja operatorowa w tym przypadku (Rys. 5) reprezentuje zarówno amplitudę jak i fazę odpowiedzi częstotliwościowej takiego systemu.
Jednym z podstawowych elementów pasywnych jest rezystor R. Jego impedancję można łatwo określić (4).
![]()
(4)
Kolejnym wymienionym elementem jest cewka L. Jej impedancję można zapisać korzystając z funkcji operatorowej (5).
![]()
(5)
Kondensator C zazwyczaj posiada pewną przewodność G (element równoległy do kondensatora) i impedancję obu elementów można go zapisać jak poniżej (6).
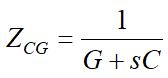
(6)
Istnieje kilka możliwych kombinacji wszystkich tych elementów. Jeśli elementy te zostaną połączone szeregowo, wtedy tworzą układ rezonansowy szeregowy (Rys. 6), gdzie elementami gromadzącymi energię są kondensator C i cewka L, natomiast rezystancja R i przewodność G odpowiadają za straty elementów C i L.
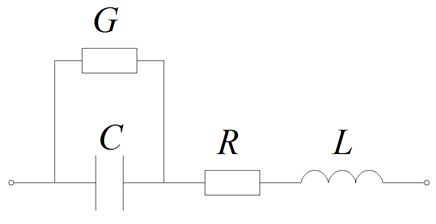
Rys. 6. Układ rezonansowy szeregowy
Dla układu rezonansowego szeregowego równanie operatorowe impedancji zastępczej Zeq można zapisać jako (7).
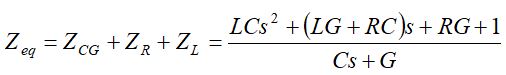
(7)
Odpowiedź częstotliwościowa takiego układu przedstawia rysunek 7. Licznik impedancji zastępczej posiada zespoloną parę zer, które określają minimum funkcji odpowiedzi częstotliwościowej.
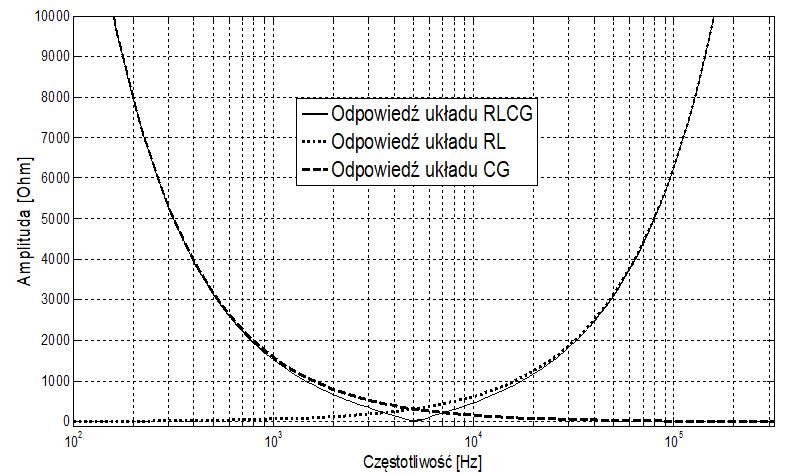
Rys. 7. Odpowiedź częstotliwościowa układu rezonansowego szeregowego
Funkcja odpowiedzi częstotliwościowej układu rezonansowego szeregowego posiada jedno minimum, dla którego można określić częstotliwość rezonansową na podstawie wzoru (8).
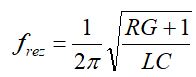
(8)
Zazwyczaj RG<<1, a więc wpływ na wartość częstotliwości rezonansowej mają głównie indukcyjność L i pojemność C.
Jeżeli elementy R, L, C, G zostaną połączone równolegle, wtedy tworzą układ rezonansowy równoległy (Rys. 8).
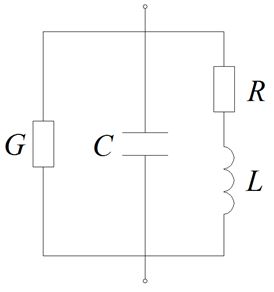
Rys. 8. Układ rezonansowy równoległy
Dla układu rezonansowego równoległego równanie operatorowe impedancji zastępczej Zeq można zapisać jako (9).
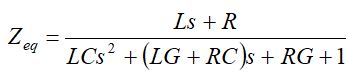
(9)
Odpowiedź częstotliwościową takiego układu przedstawia rysunek 9. Układ posiada jeden rezonans, dla którego wartość częstotliwości można także wyliczyć z równania na frez.
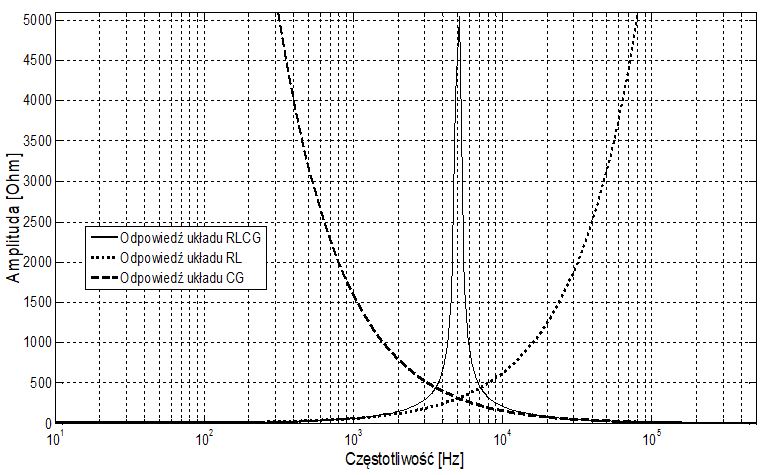
Rys. 9. Odpowiedź częstotliwościowa układu rezonansowego równoległego
W prawdziwym życiu nie ma idealnych sytuacji, dlatego powinno się wziąć pod uwagę, że rezystory produkowane są z pewną tolerancją, a także, że rezystancja zmienia się w rzeczywistości w zależności od czasu życia materiałów. Drugą rzeczą jest to, że powinno się również wziąć pod uwagę maksymalną moc rozpraszania rezystorów (10).
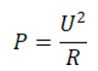
(10)
W momencie, kiedy już wszystkie elementy zostaną określone należy rozważyć odpowiednią ochronę dzielnika napięcia. Zakłada się, że urządzenie musi wytrzymać odpowiednią wartość napięcia w odpowiednim czasie. Należy zatem nie pozwolić, aby napięcie było wyższe niż wytrzymywane. Można użyć np. dwóch zabezpieczeń: rury wyładowczej (Comgap) równolegle z R2 i dwóch diod Zenera również równoległych (Rys. 10). Dioda Zenera jest dwukierunkowa, więc stanowi ochronę nie tylko dla błędów dodatnich, ale także ujemnych. W przypadku Comgap ważne jest sprawdzenie liczby operacji, ponieważ jest ograniczona. Rgap reprezentuje ochronę Comgap. Istnieją również dwie diody Zenera do ochrony. C1 i C2 reprezentują pojemności rezystorów. Cadd to dodatkowa pojemność kompensująca te C1 i C2. R2” i R2” oznaczają razem rezystancję niskiego napięcia.
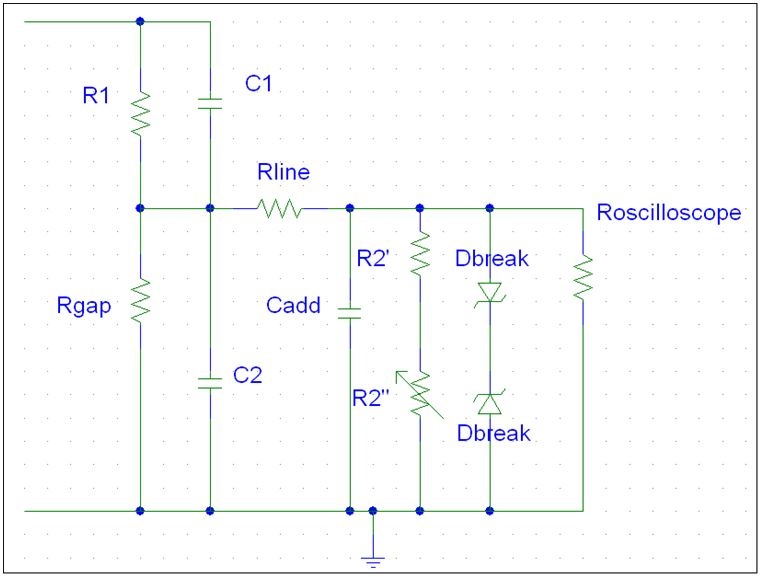
Rys. 10. Układ dzielnika napięcia z elementami zabezpieczającymi
3. Zadanie
Należy zaprojektować dzielnik napięcia o parametrach:
Przekładnia 1000:1
Max napięcie wejściowe 20kV, 40kV peak (100 ms szerokość impulsu)
Impedancja wejściowa 50MΩ i 5pF
Pasmo przenoszenia około 75 MHz
Wyjście 50Ω kabel współosiowy
Należy ponadto:
- dobrać poszczególne elementy dzielnika jako rzeczywiste (załączyć w raporcie karty katalogowe)
- dobrać przewód oscyloskopowy
- wykonać właściwy przegląd literatury (min 5 pozycji – artykułów naukowych)
- określić cenę każdego elementu bez oscyloskopu – zgodnie z tabelą
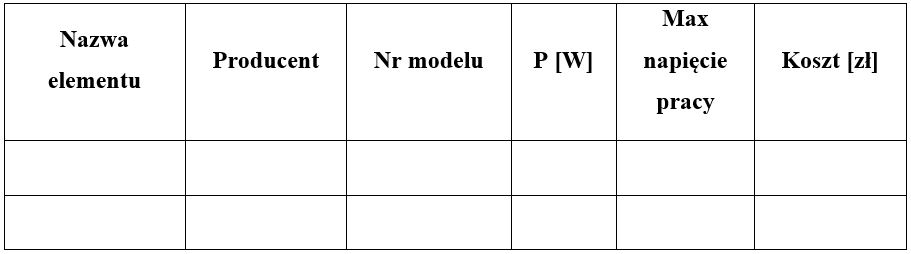
- znaleźć równanie operatorowe impedancji zastępczej dzielnika i pokazać jego odpowiedź częstotliwościową
- opisać poszczególne kroki doboru elementów i obliczenia
