1 No. 1: Measurement of luminous flux by using integrating sphere
Krzysztof Skarżyński
INTRODUCTION
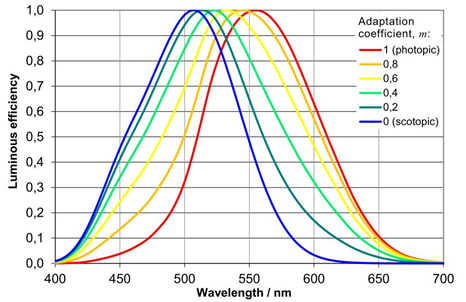
The luminous flux (1) is the photometric quantity derived from radiant flux (2) by evaluating the radiation to its action upon the standard photometric observer – the spectral luminous efficiency for photopic vision (fig. 1). The curve shown in fig. 1 (red line) is related to the spectral sensitivity of the human eye that is adapted to the high level of ambient brightness. It is characterized by the maximum (100%) of sensitivity for 555 nm. To the contrary the scotopic vision (blue line in fig.1) is connected with the sensitivity
of the human eye that is adapted to the very low level of ambient brightness. In this case, the maximum sensitivity occurs for 507 nm. The “lumen” is the unit of luminous flux in International System of Units – SI. One lumen (lm) equals one candela (cd) times one steradian (sr) (3).
where:
[latex]\partial {{Q}_{e}}[/latex] -radiant~energy [J]
[latex]t[/latex] – time [s]
[latex]{{\phi }_{e}}\left( \lambda \right)[/latex] – radiant flux [W]
[latex]\lambda[/latex] – wavelength [nm]
[latex]{{V}_{\lambda }}[/latex] – spectral luminous efficiency for photopic vision
[latex]{{K}_{m}}[/latex] – coefficient: 683 [latex]\left[ \frac{{lm}}{W} \right][/latex] for photopic vision and 1699 [latex]\left[ {~\frac{{lm}}{W}~} \right][/latex] for scotopic vision
Table 1. The exemplary values of luminous flux
| Name | Luminous flux [lm] | |
| 1. | Incandescent lamp 60W | 800 |
| 2. | Linear fluorescent lamp 14W / 3000K | 1200 |
| 3. | Metal halide lamp 35W / 3000K | 3700 |
| 4. | High pressure sodium lamp 70W | 6600 |
| 5. | LED 20W/ 4000K | 2400 |
The luminous flux is one of the most basic quantities of the light sources and lighting technology issues. It gives information about the “power of radiation” in terms of optical and vision quantities. Moreover, it is crucial to collect the knowledge about the electric power which is needed to create the particular amount of luminous flux because of the energy efficiency issue. The quantity which presents it is called luminous efficacy (4). This is another very useful parameter which allows to describe and compare different light sources within the context of rational use of the electric energy. Furthermore, it is not good practice to compare light sources only due to the luminous efficacy. The whole problem is more complicated than it looks. The typical ranges for the values of luminous efficacy for different light sources are presented in table 2.
Table 2. The typical ranges for the values of luminous efficacy for different light sources
| Name | Luminous efficacy [lm/W] | |
| 1. | Bulb | 1 – 20 |
| 2. | Fluorescent lamp | 50 – 80 |
| 3. | Metal halide lamp | 80 – 120 |
| 4. | High pressure sodium lamp | 120 – 170 |
| 5. | LEDs | 80 – 150 |
THE INTEGRATING SPHERE THEORY
The integrating sphere (Ulbricht’s sphere) is the commonly used instrument in photometry. This device was invented by R. Ulbricht at the end of the 19th Century. It is useful not only for luminous flux measurement but also for study the other parameters of light sources and luminaires e.g. luminous efficacy, light output ratio (LOR). Integrating sphere is also the main part for other instruments such as reflectance meters, spectrophotometers etc. The typical appearances of integrating spheres are presented in fig. 2. The best way to present the inside of the integrating sphere is to prepare its cross section (fig. 3).

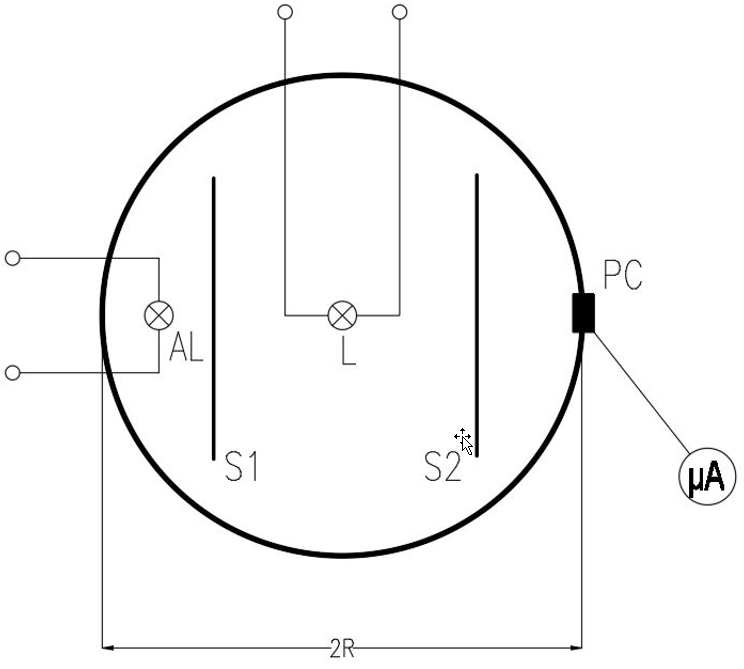
The main rule of working of this instrument is based on the Lambertian reflectance and inter-reflections. The inside surface of this instrument is covered with special type of paint (quite expensive). This paint should be characterized by the reflectance factor
ρ at least 0,8 and the reflection ought to be diffusive, and non-selective.
The illuminance E [lx] in the slot for the photovoltaic cell can be described by the sum of the direct illuminance Ed and indirect illuminance Ein which is the result of the inter-reflection in the inside of this sphere (5). However, it turned out that luminous flux φ of the light source is proportional only to the indirect illuminance Ein and inter-reflections. To eliminate direct illuminance Ed there is the need of using shutters inside the integrating sphere (6)
Furthermore, the formula (6) is quite complicated. The formula can be given in much simpler form if we use constant k which is linked to the main parameters of integrating sphere – radius R, and reflectance factor [latex]\rho[/latex] (7),(8)
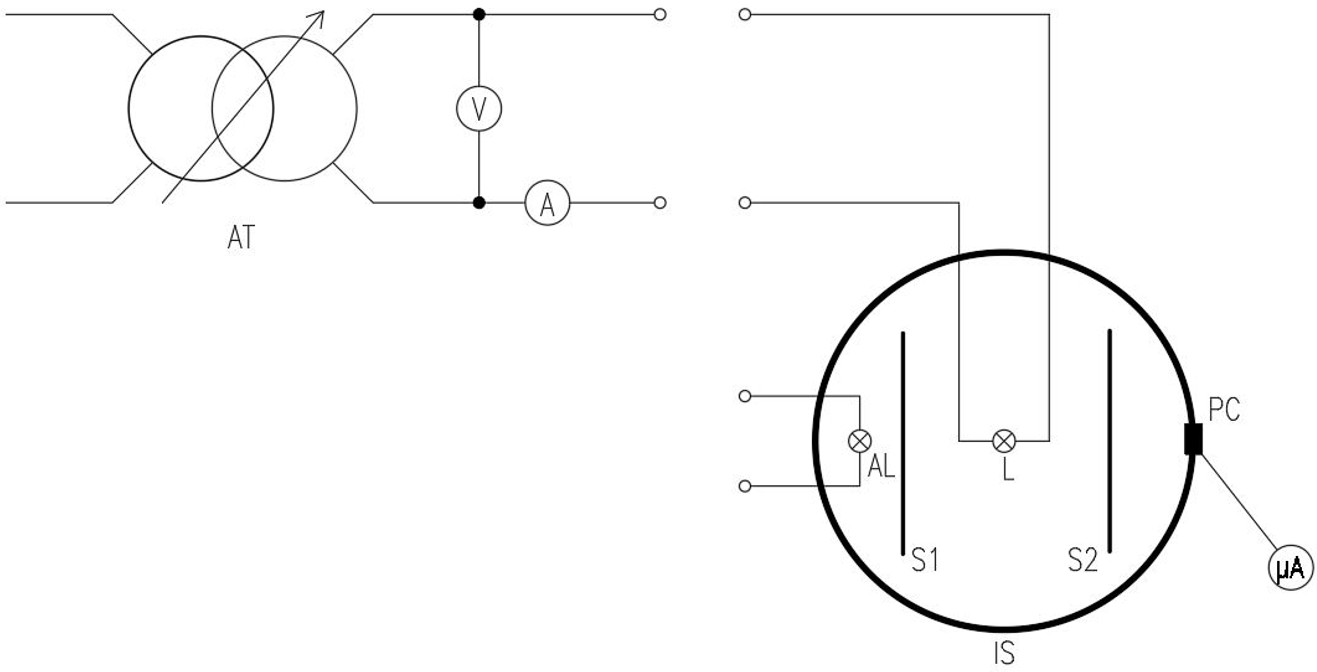
To measure luminous flux of the given sample we need to use the standard lamp. Standard lamp is the lamp that the value of luminous flux is already known. Then we need to compare the radiation of the standard lamp with the radiation of the test lamp.
The formula (8) for the standard lamp:
The formula (8) for the test lamp:
The final formula for calculation luminous flux looks like (11). It is the simple proportion between (9) and (10).
where:
[latex]{{\phi }_{x}}[/latex] – luminous flux of test lamp [lm]$
[latex]{{\phi }_{s}}[/latex] – luminous flux of standard lamp [lm]$
[latex]{{E}_{x}}[/latex] – illuminance or indication of photocurrent meter for test lamp [lm]$
[latex]{{E}_{S}}[/latex] – illuminance or indication of photocurrent meter for standard lamp [lm]$
What is more, sometimes there is the need of using the auxiliary lamp during the measurement to eliminate the systematic error that is linked with the different geometry of the standard lamp and test sample. The formula for this elimination is (12).
where:
[latex]{{\phi }_{x}}[/latex] – luminous flux of test lamp [lm],
[latex]{{\phi }_{s}}[/latex] – luminous flux of standard lamp [lm],
[latex]{{E}_{x}}[/latex] – illuminance or indication of photocurrent meter for test lamp [lm],
[latex]{{E}_{S}}[/latex] – illuminance or indication of photocurrent meter for standard lamp [lm],
[latex]{{E}_{{as}}}[/latex] – illuminance or indication of photocurrent meter for auxiliary lamp when standard lamp is inside [lm],
[latex]{{E}_{{ax}}}[/latex] – illuminance or indication of photocurrent meter for auxiliary lamp when test lamp is inside [lm].
LABORATORY TASKS
The main aim of this laboratory class is to familiarize students with the methodology of using the integrating sphere for the luminous flux measurement. Students must do the basic measurement during the time of classes according the lecturer’s instructions.
After the laboratory students must prepare a report in their groups.
The laboratory is divided into three parts:
- Selection of test samples and proper working standard lamps.
- Measurement without auxiliary lamp.
- Measurement with auxiliary lamp.
REPORT
The report from this laboratory class ought to contain the following sections:
- Short introduction about the methodology of measurement.
- Results of the measurements (of all electric and photometric quantities).
- Calculation of all necessary quantities (power, luminous flux, luminous efficacy).
- Conclusion (comparison of different light sources due to their values of luminous efficacy, comparison of the measurement with and without auxiliary lamp, other useful observation including analysis of sources of errors).
QUESTIONS FOR THE ENTRANCE TEST
- Definition of luminous flux (formula, description, unit, exemplary values).
- How does integrating sphere work (drowning, formula, methodology)?
- Definition of luminous efficacy of light source (formula, description, unit, exemplary values).
- The spectral luminous efficiency for photopic and scotopic vision (what does it stand for? drowning and wavelengths for maximum values).
- How to eliminate the systematic error connected with the different shapes of test lamp and standard lamp (formula and description of the methodology of measurement).
LITERATURE
[1] CIE Technical Note 004:2016, The Use of Terms and Units in Photometry
– Implementation of the CIE System for Mesopic Photometry, CIE, Vienna, 2016
[2] CIE Publication No 84, The measurement of luminous flux, CIE, Vienna, 1989
[3] Czyżewski , Zalewski S., Laboratorium fotometrii i kolorymetrii, OWPW, Warsaw 2007 [in polish]
[4] IESNA Lighitng Handbook, 9th edition, IESNA, New York, 2000
[5] The SLL Lighting Handbook,The Society of Light and Lighting, February 2009, ISBN 978-1-906846-02-2
[6] Żagan W., Podstawy techniki świetlnej, OWPW, Warsaw, 2014 [in polish]
