Analiza obrazu

Po etapach akwizycji i przetwarzania wstępnego możemy obraz poddać dalszej analizie. Sposób analizy jest determinowany tym, jaką informację chcemy uzyskać. W wielu zastosowaniach systemów wizyjnych, jesteśmy w stanie bardzo łatwo wskazać użyteczne parametry (cechy). Część analiz obrazu obejmuje te związane z kolorami, inne z wystąpieniem pewnego charakterystycznego wzorca. W części analiz chcemy wskazać pewne wzorce, lub obliczyć fizyczne wymiary zarejestrowanego obiektu.

Jedną z najprostszych cech obrazu jest rozkład częstości występowania pikseli o zadanym kolorze, nasyceniu lub jasności. W takim przypadku możemy jako cechę możemy zastosować histogram obrazu. Histogram przedstawia rozkład częstości występowania na przykład  jasności pikseli w całym obrazie. Częstość występowania pewnych kolorów, lub rozkład występowania kolorów może być bardzo użyteczną cechą. Aby wyznaczyć histogram, możemy posłużyć się funkcją calcHist() lub hist() z biblioteki matplotlib. Na listingu 1 zaprezentowano fragment programu, który wyznacza histogram dla obrazu kolorowego i tego samego obrazu o odcieniach szarości. Na rysunku 1 zaprezentowano obraz, dla którego obliczany jest histogram. Na rysunku 2 i 3 zaprezentowano histogramy obliczone dla obrazu o odcieniach szarości oraz dla poszczególnych składowych RGB.

Listing 1. Program prezentujący obliczanie histogramu .

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('kostka_rubicka.jpg',0)

cv2.imshow('obraz',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

plt.hist(img.ravel(),256,[0,256]); plt.show()

img = cv2.imread('kostka_rubicka.jpg')
color = ('b','g','r')
for i,col in enumerate(color):
   histr = cv2.calcHist([img],[i],None,[256],[0,256])
   plt.plot(histr,color = col)
   plt.xlim([0,256])
   plt.show()

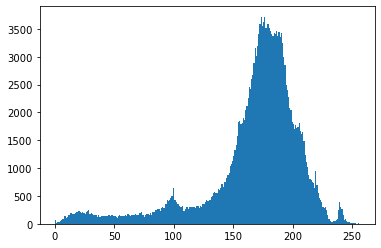
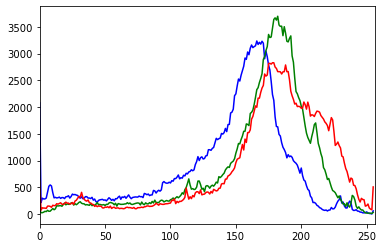
W trakcie analizy obrazu, możemy być zainteresowani wykryciem pewnego koloru na obrazie. W tym celu, możemy wybrać takie piksele, które mieszczą się w interesującej nas przestrzeni barw. W tym celu możemy wykorzystać nie tylko przestrzeń barw BGR, ale również HSV. Aby dokonać konwersji z przestrzeni BGR na HSV możemy wykorzystać funkcję cvtColor(). Następnie, wykorzystując funkcję inRange() możemy wskazać zakres interesujących nas wartości kolorów w przestrzenie HSV. W ten sposób, możemy stworzyć maskę wskazującą piksele z naszego przedziału. Na listingu 2 zaprezentowano program do wyznaczenie miejsc obrazu prezentujących kolor niebieski. Kluczem odpowiedniej selekcji kolorów jest prawidłowy dobór zakresów. Na rysunku 4 oraz 5 zaprezentowano wyniki działania programu maskę oraz obraz prezentujący wykryty kolor.

Listing 2. Program wyznaczający maskę występowania koloru niebieskiego na obrazie.

import cv2
import numpy as np

frame = cv2.imread('kostka_rubicka.jpg')

hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)

lower_blue = np.array([100,50,50])
upper_blue = np.array([240,255,255])

mask = cv2.inRange(hsv, lower_blue, upper_blue)
res = cv2.bitwise_and(frame,frame, mask= mask)

cv2.imshow('frame',frame)
cv2.waitKey(0)

cv2.imshow('mask',mask)
cv2.waitKey(0)

cv2.imshow('res',res)
cv2.waitKey(0)

cv2.imwrite('wynik_res_blue.jpg', res)
cv2.imwrite('wynik_mask_blue.jpg', mask)

cv2.destroyAllWindows()

Oprócz samych kolorów, w trakcie analizy obrazu możemy być zainteresowani wyodrębnieniem pewnych znanych wzorców/szablonów. Możemy sobie wyobrazić, że naszym wzorcem będzie fragment znanego i poszukiwanego obrazu. W takim przypadku, porównując każdy piksel naszego wzorca i obrazu, możemy obliczyć podobieństwo, na przykład z wykorzystaniem współczynnika korelacji. Jeśli poszukiwany wzorzec jest mniejszym fragmentem całości obrazu, to wzorzec możemy przesuwać co piksel po całym obrazie i obliczać współczynnik korelacji. W wyniku przesuwania wzorca i obliczenia współczynnika korelacji dla każdego obszaru, jesteśmy w stanie wskazać obszary obrazu o największej korelacji z naszym wzorcem. Pewien „wysoki” próg współczynnika korelacji, jest wskaźnikiem znalezienia obszaru zawierającego wzorzec. W zadaniu dopasowywania wzorców możemy wykorzystać funkcję matchTemplate(). Do obliczenia podobieństwa nie musimy korzystać z współczynnika korelacji (TM_CCOEFF), ale możemy wykorzystać inne miary: kwadrat różnicy (TM_SQDIFF), znormalizowana metoda porównywania kwadratu różnicy (TM_SQDIFF_NORMED), korelacja krzyżowa (TM_CCORR), znormalizowana metoda korelacji krzyżowej (TM_CORR_NORMED), znormalizowana metoda dopasowywania współczynnika korelacji (TM_CCOEFF_NORMED). Na listingu 3 zaprezentowano program, który stosując metodę dopasowywania wzorca przeszukuje obraz, wyznacza współczynniki dopasowania a następnie wskazuje potencjalne wystąpienie wzorca.

Listing 3. Program prezentujący metodę dopasowywania wzorca.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('lewandowski.jpg',0)
img2 = img.copy()
template = cv2.imread('glowa.jpg',0)
w, h = template.shape[::-1]

methods = ['cv2.TM_CCOEFF', 'cv2.TM_CCOEFF_NORMED', 'cv2.TM_CCORR',
'cv2.TM_CCORR_NORMED', 'cv2.TM_SQDIFF', 'cv2.TM_SQDIFF_NORMED']

for meth in methods:
   img = img2.copy()
   method = eval(meth)

   res = cv2.matchTemplate(img,template,method)
   min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(res)

   if method in [cv2.TM_SQDIFF, cv2.TM_SQDIFF_NORMED]:
      top_left = min_loc
   else:
     top_left = max_loc
     bottom_right = (top_left[0] + w, top_left[1] + h)

   cv2.rectangle(img,top_left, bottom_right, 255, 2)

   plt.subplot(121),plt.imshow(res,cmap = 'gray')
   plt.title('Matching Result'), plt.xticks([]), plt.yticks([])
   plt.subplot(122),plt.imshow(img,cmap = 'gray')
   plt.title('Detected Point'), plt.xticks([]), plt.yticks([])
   plt.suptitle(meth)

   plt.show()

Na rysunku 6 zaprezentowano wyniki obliczonych wartości dopasowania oraz wykrytą (najlepszą) wartość dopasowania wraz z zaznaczonym obszarem zawierającym wzorzec. Warto zwrócić uwagę, że obraz jest ładowany w odcieniach szarości. Następnie na na takim obrazie, dokonywane jest dopasowanie wzorca. W celu wizualizacji oryginalnego obrazu trzeba załadować obraz kolorowy a następnie nanieść na niego prostokąt wskazujący dopasowanie (Rysunek 7).

W trakcie analizy obrazu, możemy chcieć wykryć nie tylko jeden obiekt ale wiele obiektów. W takim przypadku musimy zaprezentować wszystkie potencjalne najlepsze punkty powyżej pewnego progu. Przykład programu prezentującego wykrycie czarnego pionka na obrazie szachownicy zaprezentowano na listingu 4.  W tym przypadku ustawiono próg wykrycia równy 0.8. Na rysunku 8 zaprezentowano sposób wykrycia poszukiwanych elementów.

Listing 4. Przykład programu prezentujący wykrycie czarnego pionka w obrazie.

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt

img_rgb = cv.imread('szachy_a.png')
img_gray = cv.cvtColor(img_rgb, cv.COLOR_BGR2GRAY)
template = cv.imread('pionek.png',0)

w, h = template.shape[::-1]
res = cv.matchTemplate(img_gray,template,cv.TM_CCOEFF_NORMED)
threshold = 0.8
loc = np.where( res = threshold)
for pt in zip(*loc[::-1]):
   cv.rectangle(img_rgb, pt, (pt[0] + w, pt[1] + h), (0,0,255), 2)

cv.imwrite('res.png',img_rgb)

Jedną z transformat, które możemy zastosować na obrazie jest transformata Fouriera. W typowej analizie sygnałów zmiennych w czasie, transformata Fouriera może posłużyć do znalezienia częstotliwości występujących w sygnale. Analiza obrazu z wykorzystaniem transformaty Fouriera pozwala na opisanie, powtarzalności w wierszach i kolumnach intensywności pikseli w obrazie. W praktyce stosujemy algorytm szybkiego przekształcenia Fouriera (FFT). Biblioteka OpenCV i numpy posiada kilka użytecznych funkcji ułatwiających obliczenie, przesunięcie oraz wizualizację wyników transformaty Fouriera. W trakcie wizualizacji wyników FFT obrazu stosujemy przesunięcie. W takim przypadku, punkt centralny wiąże się z najniższymi składowymi intensywności „powtarzalności” pikseli. Natomiast im dalej w pionie/poziomie od punktu centralnego, tym większe składowe intensywności pikseli. Wynik przedstawiamy najczęściej w postaci wartości bezwzględnej amplitudy. Na listingu 5 zaprezentowano program który oblicza transformatę Fouriera na obrazie. Na rysunku 9 przedstawiono obraz wejściowy, oraz wynik przekształcenia Fouriera.

Listing 5. Program prezentujący sposób obliczenia transformaty Fouriera na obrazie.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('star.jpg',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

cv2.imshow('wynik',magnitude_spectrum);
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imwrite('po_fft.png',magnitude_spectrum);

Interpretacja wyniku dyskretnej transformaty Fouriera na obrazie może być ciężkim zadaniem, w szczególności w początkowej fazie nauki tego zagadnienia. Istnieje szereg narzędzi i pomocy ułatwiających zrozumienie i interpretację uzyskanych wyników. W trakcie nauki warto posłużyć się pomocami takimi jak (strona internetowa: http://bigwww.epfl.ch/demo/ip/demos/FFT/ i http://www.jcrystal.com/products/ftlse/index.htm oraz  program http://www2.kobe-u.ac.jp/~kuroki/OpenSoft/FFT2D/index_en.html 2D Fast Fourier Transform Software FFT2D Stworzony na Uniwersytecie Kobe). Stworzone oprogramowanie, pozwala na przeprowadzenie serii prostych eksperymentów pozwalających na modyfikację widma i wykonanie odwrotnego przekształcenia Fouriera.

Tworząc maskę i usuwając pewne składowe o niskich lub wysokich częstotliwościach możemy „przefiltrować” obraz z pewnych składowych. Filtr dolnoprzepustowy pozwala na uzyskanie efektu rozmycia, natomiast filtr górnoprzepustowy pozwala na wskazanie krawędzi w obrazie. Przykład filtru z wykorzystaniem maskowania i usunięcia pewnych częstotliwości przedstawiono na listingu 6. Na rysunkach 10 i 11 zaprezentowano przykłady obrazów oraz wyniki przekształceń po  filtrze górno i dolno przepustowym.

Listing 6. Program przedstawiający możliwości modyfikacji transformaty Fouriera.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('szachy.png',cv2.IMREAD_GRAYSCALE)
img = cv2.resize(img,(len(img[0])//2,len(img)//2))

rows, cols = img.shape
crow,ccol = rows/2 , cols/2

dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)


mask = np.zeros((rows,cols,2),np.uint8)
mask[round(crow)-30:round(crow)+30, round(ccol)-30:round(ccol)+30] = 1
#mask = 1-mask


fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Output Image'), plt.xticks([]), plt.yticks([])
plt.show()

Innym ważnym zagadnieniem, jest wykrycie prostych kształtów w obrazie takich jak linia lub okrąg. W takim zadaniu możemy wykorzystać transformatę Hougha. Transformata jest relatywnie szybką metodą wyszukiwania kształtów. Jednak wymaga przeszukania wszystkich możliwych prostych/okręgów na obrazie. Dla przykładu, każda prostą możemy przedstawić jako jej kąt nachylenia oraz punkt przecięcia z osią współrzędnych. Jeśli dla każdej możliwej prostej, zsumujemy potencjalne punkty niezerowe obrazu leżące na tej prostej to możemy wykryć potencjalne linie. W praktyce, aby wykorzystać transformatę należy skorzystać z gotowych funkcji do detekcji linii HoughLines() oraz HoughCircles(). W trakcie znalezienia potencjalnych kształtów kluczowe są parametry wejściowe funkcji. Przed transformatą Hougha stosuje się najczęściej wykrycie krawędzi. Na listingu 7 zaprezentowano program wykrywający linie. Na rysunku 12 zaprezentowano pośredni etap wykrycia linii- obraz po wykryciu krawędzi. Na rysunku 13 zaprezentowano obraz z wykrytymi liniami.

Lisnting 7. Program wykrywający linie z wykorzystaniem transformaty Hougha.

import cv2
import numpy as np

dave = cv2.imread('szachownica.png')
dave1 = cv2.cvtColor(dave,cv2.COLOR_BGR2GRAY)
dave2 = cv2.Canny(dave1,100,200,apertureSize = 3)

cv2.imshow('image',dave2)
cv2.waitKey(0)
cv2.destroyAllWindows()

lines = cv2.HoughLines(dave2,1,np.pi/20,500)

for linea in lines:
   for rho,theta in linea:
      a = np.cos(theta)
      b = np.sin(theta)
      x0 = a*rho
      y0 = b*rho
      x1 = int(x0 + 1000*(-b))
      y1 = int(y0 + 1000*(a))
      x2 = int(x0 - 1000*(-b))
      y2 = int(y0 - 1000*(a))

    cv2.line(dave,(x1,y1),(x2,y2),(0,0,255),3)

cv2.imshow('image',dave)
cv2.waitKey(0)
cv2.destroyAllWindows()

Aby wykonać detekcję okręgów należy wykorzystać funkcję HoughCircles(). Zamiast wykrycia krawędzi możemy zastosować filtr rozmycia. Przykład wykrycia okręgów na obrazie zaprezentowano na listingu 8. Obraz wejściowy na którym chcemy dokonać detekcji zaprezentowano na rysunku 14. Na rysunku 15 zaprezentowano wykryte okręgi. Aby wykryć okręgi kluczowe są parametry detekcji param1=150, param2=130, minRadius=50, maxRadius=500. Zmieniając parametry możemy zawęzić lub rozszerzyć zakres poszukiwanych obiektów.

Listing 8. Program prezentujący wykrycie okręgów na obrazie.

import cv2
import numpy as np

img = cv2.imread('rower_a.png',0)
img = cv2.medianBlur(img,5)
cimg = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)

cv2.imshow('detected circles',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,200,
param1=150,param2=130,minRadius=50,maxRadius=500)

circles = np.uint16(np.around(circles))
for i in circles[0,:]:
cv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)
cv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3)

cv2.imshow('detected circles',cimg)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('wynik_detekcji.png',cimg)

Zadanie 1.

Dla obrazu zaprezentowanego na Rysunku 1 przedstawiającego układanie kostki Rubicka, proszę wykryć kolor czerwony a następnie kolor zielony. Proszę zmodyfikować program tak, aby zapisywał w pliku graficznym maskę wykrytego koloru.

Odpowiedź 1.

Należy zmodyfikować fragment programu zaprezentowanego na listingu 2. Modyfikacji należy dokonać zaprezentowanych poniżej. Aby ułatwić dobór zakresu parametrów kolorów w przestrzeni HSV można użyć ogólnodostępnego kalkulatora/konwertera przestrzeni barw (https://www.rapidtables.com/convert/color/rgb-to-hsv.html https://www.peko-step.com/en/tool/hsvrgb_en.html).

lower_blue = np.array([100,50,50])
upper_blue = np.array([240,255,255])
mask = cv2.inRange(hsv, lower_blue, upper_blue)
res = cv2.bitwise_and(frame,frame, mask= mask)

Zadanie 2.

Proszę wyznaczyć histogramy dla kilku obrazów: krajobrazu, znaku graficznego, fotografii prezentującej twarz, znak drogowy. Należy zaprezentować histogramy dla obrazu o odcieniach szarości oraz histogramu dla kolejnych składowych BGR.

Odpowiedź 2.

Program obliczający histogramy zaprezentowano na listingu poniżej.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('obraz_wejsciowy.jpg',0)

cv2.imshow('obraz',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

plt.hist(img.ravel(),256,[0,256]); plt.show()

img = cv2.imread('kostka_rubicka.jpg')
color = ('b','g','r')
for i,col in enumerate(color):
   histr = cv2.calcHist([img],[i],None,[256],[0,256])
   plt.plot(histr,color = col)
   plt.xlim([0,256])
   plt.show()

Zadanie 3.

Proszę zaimplementować program wyszukujący białe pionki na szachwonicy. Jako obraz wejściowy proszę zastosowac obraz szachownicy z Rysunku 7.

Odpowiedź 3.

Należy stworzyć wzorzec prezentujący fragment obrazu zawierający biały pionek. Następnie należy wykorzystać program zaprezentowany na listingu 4.

Zadanie 4.

Proszę zaimplementować program oraz dostosować parametry w celu wykrycia linii na obrazach przedstawiających: drogę wraz z pasami ruchu, znak graficzny zawierający linie.

Odpowiedź 4.

Należy zmodyfikować program na listingu poniżej. Należy dobrać parametry funkcji HoughLines().

import cv2
import numpy as np

dave = cv2.imread('grafika.png')
dave1 = cv2.cvtColor(dave,cv2.COLOR_BGR2GRAY)
dave2 = cv2.Canny(dave1,100,200,apertureSize = 3)

cv2.imshow('image',dave2)
cv2.waitKey(0)
cv2.destroyAllWindows()

lines = cv2.HoughLines(dave2,1,np.pi/20,500)

for linea in lines:
   for rho,theta in linea:
      a = np.cos(theta)
      b = np.sin(theta)
      x0 = a*rho
      y0 = b*rho
      x1 = int(x0 + 1000*(-b))
      y1 = int(y0 + 1000*(a))
      x2 = int(x0 - 1000*(-b))
      y2 = int(y0 - 1000*(a))

      cv2.line(dave,(x1,y1),(x2,y2),(0,0,255),3)

cv2.imshow('image',dave)
cv2.waitKey(0)
cv2.destroyAllWindows()

Zadanie 5.

Proszę zaimplementować program oraz dostosować parametry w celu wykrycia okręgów na obrazach przedstawiających: monety, źrenicę oka, grafikę zawierającą okręgi o różnej średnicy i kolorze .

Odpowiedź 5.

Należy zmodyfikować program na listingu poniżej. Należy dobrać parametry funkcji HoughCircles().

import cv2
import numpy as np

img = cv2.imread('rower_a.png',0)
img = cv2.medianBlur(img,5)
cimg = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)

cv2.imshow('detected circles',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,200,
param1=150,param2=130,minRadius=50,maxRadius=500)

circles = np.uint16(np.around(circles))
for i in circles[0,:]:

cv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)

cv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3)

cv2.imshow('detected circles',cimg)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('wynik_detekcji.png',cimg)