Metody przetwarzania obrazu

Zarejestrowany obraz możemy poddać całemu szeregowi przekształceń. Jednym z rodzajów takich przekształceń są transformacje afiniczne. Transformacje afiniczne mogą być stosowane, gdy mamy obraz z obszarem zainteresowania (ROI), który chcemy przekształcić, albo gdy mamy listę punktów, dla których obliczyć wynik przekształcenia. W praktyce, aby zastosować przekształcenie musimy obliczyć macierz przekształceń M, która reprezentuje transformację.

Pierwszym przykładem jest możliwość przekształcenia obrazu, na podstawie trzech punktów, które chcemy transformować. Do obliczenia macierzy M, na podstawie punktów służy funkcja getAffineTransform(). Przykład programu stosujący transformację zaprezentowano na listingu 1. Na wejściu funkcji musimy zdefiniować współrzędne trzech punktów przed i po transformacji. Do zastosowania transformacji służy funkcja warpAffin(). Na wejściu funkcji podajemy obraz, który chcemy poddać transformacji, macierz M, oraz rozmiar wyjściowy obrazu.  Dla obliczonej raz macierzy M możemy przekształcić wiele obrazów. Wzór transformacji można opisać:  dst(x,y)=src(M11x+M12y+M13,M21x+M22y+M23). Na rysunku 1 zaprezentowano wynik transformacji oraz obraz wejściowy. Dla ułatwienia interpretacji działania, zastosowano funkcję matplotlib opisującą wiersze i kolumny obrazu. W celu przełączania miejsca wyświetlania z wykorzystaniem biblioteki matplotlib można wykorzystać opcje: %matplotlib qt oraz %matplotlib inline.

Listing 1. Zastosowanie transformacji afinicznej.

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('szachownica.png')
rows,cols,ch = img.shape

pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])

M = cv2.getAffineTransform(pts1,pts2)
dst = cv2.warpAffine(img,M,(cols,rows))

plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

Kolejnym przekształceniem afinicznym jest obrót. W tym przypadku do obliczenia macierzy M wykorzystujemy funkcję getRotationMatrix2D(). Na listingu 2 zaprezentowano przykład działania transformacji obrotu. Funkcja wymaga podania  punktu wokół którego nastąpi obrót, kąt obrotu oraz skalę obrazu wyjściowego. Dla zastosowanego przypadku macierz M=  1.73648178e-01, 9.84807753e-01, -5.07058978e+01; -9.84807753e-01, 1.73648178e-01, 5.79571064e+02. Na rysunku 2 przedstawiono przykład rotacji obrazu.

Listing 2. Zastosowanie transformacji obrotu.

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('szachownica.png')
rows,cols,b = img.shape

M = cv2.getRotationMatrix2D((cols/2,rows/2),80,1)
dst = cv2.warpAffine(img,M,(cols,rows))

cv2.imshow('dst',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('szachownica_obrot.png',dst);

plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

Innym rodzajem przekształceń, są transformacje perspektywy. W tym przypadku, do obliczenia macierzy M stosujemy funkcję getPerspectiveTransform a do przekształcenia funkcję wrapPerspective. Nowe wartości obliczane są z wykorzystaniem wzoru dst(x,y)=src((M11x+M12y+M13)/(M31x+M32y+M33), (M21x+M22y+M23)/(M31x+M32y+M33)). Przykład transformacji zaprezentowano na listingu 3. W przypadku zmiany perspektywy wymagane jest podanie czterech punktów. Wynik przykładowej transformacji zmiany perspektywy zaprezentowano na rysunku 3.

Listing 3. Przykład transformacji perspektywy.

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('szachownica.png')
rows,cols,ch = img.shape

pts1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts2 = np.float32([[0,0],[500,0],[0,500],[300,300]])

M = cv2.getPerspectiveTransform(pts1,pts2)

dst = cv2.warpPerspective(img,M,(300,300))

plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

Istnieją inne, bardziej zaawansowane transformacje. W tym celu możemy wykorzystać funkcje bibliotekiOpenCV. Dla przykładu, funkcja cartToPolar() służy do konwersji współrzędnych kartezjańskich na biegunowe, funkcja polarToCart() służy do konwersji współrzędnych biegunowych na kartezjańskie. Funkcja logPolar() jest wykorzystywana do przekształceń logarytmiczno-biegunowych. Warto zwrócić uwagę na inną funkcję remap(), która umożliwia ogólne odwzorowanie obrazu.

W trakcie rejestracji obrazu, może się zdarzyć, że fragment obrazu jest niepoprawnie zarejestrowany. Jeśli taka sytuacja ma miejsce, a są to niewielkie ubytki, możemy zastosować technikę renowacji obrazów znaną jako inpainting. Przykład takiego ubytku możemy zaobserwować na rysunku 4.  W celu odzyskania fragmentów obrazu możemy zastosować technikę inpaintingu. W tym celu możemy zastosować funkcję inpaint(). Aby funkcja mogła odzyskać piksele, które zostały usunięte, należy wskazać maskę reprezentującą piksele do odzyskania. Program, który wykorzystuje technikę inpaintingu przedstawiono na listingu 4. Funkcja inpaint przyjąć może opcje odzyskiwania INPAINT_NS oraz INPAINT_TELEA. W uproszczeni, technika inpaintingu polega na uwzględnieniu kolorów oraz tekstury na krawędziach ubytku i wypełnieniu miejsc obrazu z ubytkiem. Wynik po zastosowaniu inpaintingu zaprezentowano na rysunku 5.

Listing 4. Program prezentujący technikę inpaintingu.

import numpy as np
import cv2 as cv

img = cv.imread('owoce_mix.jpg')
mask = cv.imread('owoce_maska_a.png',0)
mask2 = cv.bitwise_not(mask)

dst = cv.inpaint(img,mask2,3,cv.INPAINT_TELEA)

cv.imwrite('owoce_odtworzony.jpg',dst);

cv.imshow('dst',dst)
cv.waitKey(0)
cv.destroyAllWindows()

Część operacji na obrazie to operacje polegające na filtracji obrazów. Filtr to algorytm który pewien obraz I(x,y) przekształca w obraz I'(x,y) poprzez obliczanie dla każdego piksela x,y w I’ pewnej funkcji pikseli z I, które znajdują się w niewielkim obszarze wokół tego punktu (x,y). Szablon który definiuje ten obszar i sposób postępowania nazywamy filtrem albo jądrem. Każdy filtr liniowy możemy opisać operacją splotu. Oczywiście kluczem pozostaje dobranie poszczególnych wag filtra. Każde z jąder ma jedną wartość, tzw. punkt centralny, który określa sposób położenia jądra względem obrazu źródłowego. W trakcie stosowania filtrów pojawia się pewna kwestia jak postępować z pikslami na krawędzi obrazu. W przypadku biblioteki OpenCV tworzone są wirtualne krawędzie.

Ważną operacją jest progowanie, obszarów obrazu. W zadaniu tym chcemy progować pewne wartości pikseli. Na listingu 5 przedstawiono program, który dokonuje progowania obrazu wejściowego dla progu 100, 150 oraz 127. W zadaniu progowania możemy wykorzystać funkcję treshold(). Funkcja może progować obraz na kilka sposóbów: THRESH_BINARY, THRESH_BINARY_INV, THRESH_TRUNC  .

Listing 5. Program prezentujący różne rodzaje progowania.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('obraz_szary.jpg',0)

ret1,th1 = cv2.threshold(img,100,255,cv2.THRESH_BINARY)
ret2,th2 = cv2.threshold(img,100,255,cv2.THRESH_BINARY_INV)
ret3,th3 = cv2.threshold(img,150,255,cv2.THRESH_TRUNC)
ret4,th4 = cv2.threshold(img,150,255,cv2.THRESH_TOZERO)
ret5,th5 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO_INV)

plt.subplot(2,3,1),
plt.imshow(img,'gray')
plt.title('Obraz wejsciowy');
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,2),
plt.imshow(th1,'gray')
plt.title('THRESH_BINARY');
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,3),
plt.imshow(th2,'gray')
plt.title('THRESH_BINARY_INV');
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,4),
plt.imshow(th3,'gray')
plt.title('THRESH_TRUNC');
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,5),
plt.imshow(th4,'gray')
plt.title('THRESH_TOZERO');
plt.xticks([]), plt.yticks([])

plt.subplot(2,3,6),
plt.imshow(th5,'gray')
plt.title('THRESH_TOZERO_INV');
plt.xticks([]), plt.yticks([])

plt.show()

Inną metodą progowania jest metoda Otsu. Metoda Ostu sprawdza wszystkie wartości graniczne i oblicza wariację dla każdej z klas pikseli poniżej i powyżej progu. Następnie dobiera próg tak aby zminimalizować sumę wariancji dla poszczególnych klas. Aby zastosować tą metodę należy zastosować opcję TRESH_OTSU. Oprócz powyższych metod istnieje jeszcze adaptacyjna technika progowania. Do tego celu należy wykorzystać funkcję adaptiveTreshold().  Funkcja dostraja próg w zależności od wybranego obszaru rejonu. Dla każdego obszaru liczona jest średnia ważona (TRESH_MEAN_C) lub odległość w rozkładzie Gaussa od punktu centralnego (ADAPTIVE_TRESH_GAUSSIAN_C).

Ważnym elementem przetwarzania obrazów są filtry wygładzające i rozmywające obraz. Najczęściej mają znaczenie w przypadku redukcji szumów lub artefaktów aparatu fotograficznego/kamery. W tym celu możemy wykorzystać funkcję blur(), służącą do rozmycia. Piksel na wyjściu jest średnią pikseli w wybranym oknie. Rozmazanie jest pewną wersją filtra prostokątnego. Oprócz filtra u uśredniającego możemy zastosować filtr medianowy, w tym celu możemy wykorzystać funkcję medianBlur(). W praktyce, bardzo często wykorzystujemy filtr Gaussa. Filtrowanie polega na obliczeniu splotu dla każdego piksela w tablicy wejściowej z znormalizowanym jądrem gaussowskim – funkcja GaussianBlur(). Innym rodzajem filtra jest filtr bileteralny. Filtr ten służy do wygładzania z zachowaniem krawędzi. Ważnym elementem wpływającym na skuteczność filtracji oraz uzyskane efekty są szczegółowe parametry poszczególnych funkcji. W wielu przypadkach, skuteczność możemy porównać poprzez sprawdzenie działania funkcji dla kilku/kilkunastu parametrów.

Listing 6. Program prezentujący działanie różne rodzaje filtrów.

import cv2
import numpy as np

img = cv2.imread('cat.jpg')

cv2.imshow('oryginal',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

kernel = np.ones((5,5),np.float32)/25
dst = cv2.filter2D(img,-1,kernel)

cv2.imshow('dst',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('1_filtr.png',dst);

blur = cv2.GaussianBlur(img,(25,5),0)
cv2.imshow('blur',blur)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('2_filtr.png',blur);

median = cv2.medianBlur(img,21)
cv2.imshow('median',median)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('3_filtr.png',median);

Oprócz filtrów dolnoprzepustowych – wygładzających możemy stosować filtry górnoprzepustowe. Najczęściej filtry te służą do wykrywania krawędzi na obrazie. W zadaniu filtracji możemy wykorzystać filtr Sobela – funkcja Sobel; filtr Sharra oraz Laplace’a – funkcja Laplacian();

Listing 7. Zastosowanie filtrów górnoprzepustowych.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('sudoku.jpg',0)

laplacian = cv2.Laplacian(img,cv2.CV_64F)
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=5)
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=5)

plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,2),plt.imshow(laplacian,cmap = 'gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,3),plt.imshow(sobelx,cmap = 'gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,4),plt.imshow(sobely,cmap = 'gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])

plt.show()

Ważnym aspektem przetwarzania obrazów są przekształcenia morfologiczne. Zasadniczo wszystkie operacje bazują na dwóch podstawowych działaniach zwanych dylatacją i erozją. Operacje te są wykorzystywane do usuwania szumu oraz ekstrakcji indywidualnych elementów oraz łączenia rozdzielonych elementów obrazu. Dylacja to pewnego rodzaju splot, w którym każdy piksel jest zamieniany na lokalne maksimum wszystkich pikseli obejmujących dane jądro. Dylatacji powoduje, że obszary rozrastają się. Operacja erozji, jest operacją odwrotną do dylatacji.  W trakcie działania operacji erozji wykonywany jest splot, w którym każdy piksel jest zamieniany na lokalne minimum wszystkich pikseli obejmujących dane jądro. Efektem operacji erozji jest pomniejszenie obszaru. Operacje erozji oraz dylatacji możemy wykonać kilkukrotnie poprzez ustawienie opcji iterations. Na listingu 9 zaprezentowano przykład operacji erozji dla obrazu prezentującego biały znak na czarnym tle.

Listing 8. Program prezentujący operację dylatacji

import cv2
import numpy as np

img = cv2.imread('j.png',0)
kernel = np.ones((5,5),np.uint8)
dilation = cv2.dilate(img,kernel,iterations = 1)

cv2.imshow('oryg',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imshow('po dylatacji',dilation)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imwrite('po_dylatacji.png',dilation);

Listing 9. Program prezentujący operację dylatacji

import cv2
import numpy as np

img = cv2.imread('j.png',0)
kernel = np.ones((5,5),np.uint8)
erosion = cv2.erode(img,kernel,iterations = 2)

cv2.imshow('oryg',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imshow('erozja',erosion)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imwrite('po_erozji_2.png',erosion);

Bazując na tych dwóch podstawowych operacjach możemy tworzyć bardziej zaawansowane operacje morfologiczne takie jak otwieranie oraz zamykanie. Do zastosowania operacji możemy wykorzystać funkcję morphologyEX. Otwieranie stosuje się między innymi w przypadku policzenia obszarów na obszarze logicznym. Technikę zamykania wykorzystuje się w bardziej zaawansowanych algorytmach przetwarzających połączone komponenty w celu redukcji niechcianych lub zawierających szum fragmentów.

Listing 10. Zastosowanie operacji zamknięcia.

import cv2
import numpy as np

img = cv2.imread('j_closing.png',0)
kernel = np.ones((5,5),np.uint8)
closing = cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel)

cv2.imshow('oryg',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imshow('closing',closing)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imwrite('po_zamknieciu.png',closing);

Listing 11. Zastosowanie operacji otwarcia.

import cv2
import numpy as np

img = cv2.imread('j_open.png',0)
kernel = np.ones((5,5),np.uint8)
opening = cv2.morphologyEx(img, cv2.MORPH_OPEN, kernel)

cv2.imshow('oryg',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imshow('opening',opening)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imwrite('po_otwarciu_2.png',opening);

Rysunek 15. Wyniki operacji otwarcia.

Ważnym aspektem przetwarzania obrazów może być wyrównanie histogramu. Histogram opisuje rozkład poziomów jasności w obrazie. Może się zdarzyć, że układ optyczny lub matryca nie poradzą sobie z uchwyceniem interesujących nas poziomów jasności. Pomóc może wyrównanie histogramu. Polega ono na tym, aby występujące w zarejestrowanym obrazie odcienie jasności obrazu, przeskalować/przekształcić tak aby mieściły się w całym zakresie 0-255. Biblioteka OpenCV posiada funkcję  equalizeHist() któa umożliwia automatyczne wyrównanie histohramu. Na listingu 12 zaprezentowano program wyrównujący histogram zajęcia. Na Rysunku 16 zaprezentowano zdjęcie przed i po zastosowaniu operacji wyrównania histogramu.

Listing 12. Przykład wyrównania histogramu.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('krajobraz_hist.jpg',0)

hist,bins = np.histogram(img.flatten(),256,[0,256])

cdf = hist.cumsum()
cdf_normalized = cdf * hist.max()/ cdf.max()

plt.plot(cdf_normalized, color = 'b')
plt.hist(img.flatten(),256,[0,256], color = 'r')
plt.xlim([0,256])
plt.legend(('cdf','histogram'), loc = 'upper left')
plt.show()

img = cv2.imread('krajobraz_hist.jpg',0)
equ = cv2.equalizeHist(img)
res = np.hstack((img,equ)) 
cv2.imwrite('res.png',res)

Zadanie 1.

Dla zdjęcia zaprezentowanego na rysunku 17, proszę zaproponować serię przekształceń obrazu, które w wyniku którego otrzymamy obraz tablicy rejestracyjnej zaprezentowanej na rysunku 18.

Odpowiedź 1.

Należy zastosować transformacje afiniczną, zmianę perepektywy, obrotu. W tym celu wykorzystujemy funkcje: getAffineTransform, warpAffine, getRotationMatrix2D, warpPerspective. Należy dobrać odpowiednio paremetry funkcji. Na otrzymane rezultaty, może mieć wpływ kolejność wykonywania przekształceń.

Zadanie 2.

Wybierz kilka różnorodnych obrazów takich jak: krajobraz, twarz, stare uszkodzone zdjęcie. Następnie przygotuj maski i spróbuj odzyskać framgenty uszkodzonych zdjęć z wykorzystaniem techniki inpaintingu. Zwróć uwagę, czy na jakośc odzyskanego zdjęcia wpływa jednorodność struktury obrazu.

Odpowiedź 2.

Na listingu 13 zaprezentowano fragment programu wykorzystujący technikę inpaintingu.

 
import numpy as np 
import cv2 as cv 
img = cv.imread('zdjecie_uszkodzone.jpg')
mask = cv.imread('maska_dla_zdjecia.png',0)
mask2 = cv.bitwise_not(mask) 
dst = cv.inpaint(img,mask2,3,cv.INPAINT_TELEA) 
cv.imwrite('obraz_odtworzony.jpg',dst); 
cv.imshow('dst',dst) 
cv.waitKey(0) 
cv.destroyAllWindows() 

Zadanie 3.

Sprawdź jak wpływa wielkość maski, jego rozmiar na wyniki filtracji. W tym celu wykorzystaj funkcję filter2D. Przeprowadź eksperymenty dla kilku obrazów i kilku stworzonych przez sibie filtrów.

Odpowiedź 3.

Aby stworzyć własny filtr należy wykorzystać funkcję filter2D. Przykłąd stworzenia filtru o rozmawrze 15×2 przedstawiono na listingu 14.

kernel = np.ones((15,2),np.float32)/30
dst = cv2.filter2D(img,-1,kernel)

Zadanie 4.

Dla obrazu otrzymanego w zadaniu 1, proszę wykonać następujące operację: proszę zwiększyć rozdzielczość obrazu, a następnie przetestować różne metody prgowania w celu, stworzenia jak najlepszego obrazu tablicy rejestracyjnej.

Odpowiedź 4.

Do przeskalowania obrazu należy wykorzystać funkcję resize(). Przykłąd listingu sprawdzającego różne metody progorania zaprezentowano na listingu 3.

Zadanie 5.

Dla zarejestrowanego zdjęcia (podejrzenie czerniaka), proszę zaproponować metodę przetwarzania wstępnego, która stworzy maskę obszaru zawierającego podejrzane znamię. Proszę dobrać parametry poszczególnych metod przetwarzania.

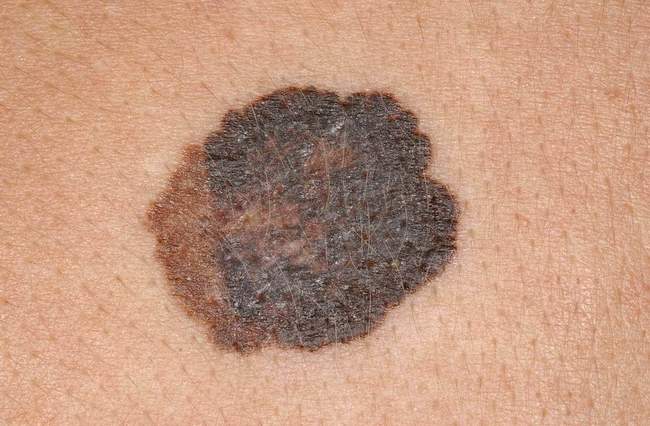
Odpowiedź 5.

Propozycję przetwarzania obrazu może obejmować: wczytanie obrazu w odciecniach szarości, progowanie metodą Otsu a następnie wykonanie erzozji. Na listingu 15 zaprezentowano program, prezentujący działanie szpozególnych etapów przetwarzania obrazów.

Listing 15. Przykład programu do wyznaczania obszaru czerniaka.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('czerniak.jpg',0)

blur = cv2.GaussianBlur(img,(5,5),0)
ret3,th3 = cv2.threshold(blur,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)

cv2.imshow('oryg',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.imshow('th3',th3)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('po_progowaniu_otsu.png',th3);

kernel = np.ones((5,5),np.uint8)
erosion = cv2.erode(th3,kernel,iterations = 2)

cv2.imshow('po erozji',erosion)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite('po_erozji_czerniak_2.png',erosion);