Zjawisko rezonansu napięć w obwodzie szeregowym RLC przy wymuszeniu sinusoidalnym i okresowym odkształconym
Wprowadzenie Teoretyczne
Radosław Roszczyk and Krzysztof Siwek
Zjawiskiem rezonansu nazywamy taki stan obwodu RLC, w którym prąd i napięcie są ze sobą w fazie. W stanie rezonansu przesunięcie fazowe prądu i napięcia jest zerowe, co oznacza, że argument impedancji lub admitancji zespolonej obwodu jest także równy zeru. Obwód nie pobiera żadnej mocy biernej a ściśle mówiąc następuje zjawisko kompensacji tej mocy. Moc bierna indukcyjna obwodu jest równa mocy pojemnościowej. Ponieważ znaki mocy biernej indukcyjnej i pojemnościowej są przeciwne, w warunkach rezonansu całkowita moc bierna jest zerowa.
Rezonans napięć w obwodzie RLC przy wymuszeniu sinusoidalnym
W obwodzie szeregowym RLC w stanie rezonansu reaktancja wypadkowa obwodu jest równa zeru. W obwodzie równoległym w stanie rezonansu część urojona admitancji (czyli admitancja) była równa zeru. Częstotliwość, przy której część urojona impedancji lub admitancji obwodu znika jest nazywana częstotliwością rezonansową.
Rezonans wystąpić może w dowolnej konfiguracji elementów RLC, warunkiem rezonansu zawsze jest przyrównanie do zera impedancji zastępczej obwodu (dla rezonansu szeregowego) lub przyrównanie do zera admitancji zastępczej obwodu (dla rezonansu równoległego).
Rezonans występujący w obwodzie, w którym elementy R, L, C są połączone szeregowo nazywamy rezonansem napięć lub rezonansem szeregowym. W przypadku, gdy rezonans dotyczy obwodu równoległego R, L, C taki rezonans nazywamy rezonansem prądów lub rezonansem równoległym. Rysunek 1 przedstawia szeregowy obwód rezonansowy RLC.
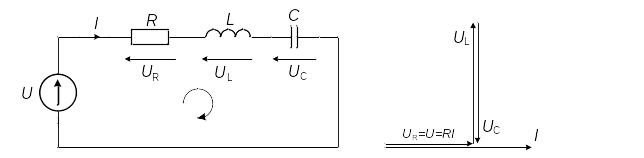
Dla obwodu szeregowego
[latex]U=U_{R} +U_{L} +U_{C} =[ R+j( X_{L} -X_{C})] I=ZI[/latex]
Rezonans wystąpi wtedy, gdy Φ=0, czyli reaktancja obwodu X=0. Odpowiada to warunkowi
[latex]Im( Z) =0[/latex]
[latex]X_{L} =X_{C}[/latex] lub [latex]\omega L=\frac{1}{\omega C}[/latex]
Częstotliwość, przy której jest spełniony ten warunek jest częstotliwością rezonansową obwodu i wynosi
[latex]f_{0} =\frac{1}{2\pi \sqrt{LC}}[/latex]
a pulsacja rezonansowa
[latex]\omega _{0} =\frac{1}{\sqrt{LC}}[/latex]
W obwodzie szeregowym dobrocią nazywamy stosunek napięcia na elemencie reaktancyjnym (cewce lub kondensatorze) do napięcia na elemencie rezystancyjnym w stanie rezonansu (dla częstotliwości rezonansowej).
[latex]Q=\frac{U_{L}}{U_{R}} =\frac{U_{C}}{U_{R}} =\frac{\omega _{0} L}{R} =\frac{1}{\omega _{0} C}[/latex]
Rysunek 2 przedstawia wykresy wektorowe dla obwodu szeregowego RLC i odpowiadające im dwójniki obwodu rezonansowego RLC dla różnych częstotliwości. Stanom tym można przypisać obwody zastępcze przedstawione na rysunku.
- częstotliwość mniejsza od rezonansowej ω<ω0 — charakter indukcyjny obwodu,
- częstotliwość rezonansowa ω=ω0 — obwód ma charakter rezystancyjny,
- częstotliwość większa od rezonansowej ω>ω0 — charakter pojemnościowy obwodu.
Rozkład funkcji okresowej na szereg Fouriera
Twierdzenie Fouriera
Każdą funkcję okresową f(t) o okresie T można przedstawić w postaci szeregu (sumy) utworzonego ze składowej stałej oraz funkcji sinusoidalnych o częstotliwościach kf ([latex]f=\frac{1}{T}[/latex]) jeśli funkcja ta spełnia warunki Dirichleta, czyli w przedziale 0-T jest bezwzględnie całkowalna, czyli:
[latex]\int\limits _{T}| f( t)| dt< \infty[/latex]
oraz ma skończoną liczbę maksimów i minimów; i co najwyżej skończoną liczbę punktów nieciągłości tk, przy czym w każdym punkcie nieciągłości istnieją skończone granice prawostronna i lewostronna a wartość funkcji w tym punkcie przyjmuje się jako średnią arytmetyczną granicy lewo- i prawostronnej, to jest:
[latex]f( t_{k}) =\frac{1}{2}[ f( t_{k-}) +f( t_{k+})][/latex]
Szereg taki jest szeregiem trygonometrycznym Fouriera.
Okres harmonicznej podstawowej jest identyczny z okresem przebiegu niesinusoidalnego f(t). Częstotliwości kolejnych harmonicznych są wielokrotnością częstotliwości harmonicznej podstawowej, czyli ωk=kω.
