Wprowadzenie Teoretyczne

Układem trójfazowym nazywamy połączony galwanicznie układ trzech obwodów elektrycznych, w których istnieją trzy źródła napięć sinusoidalnych o takiej samej amplitudzie, jednakowej częstotliwości, przesunięte względem siebie o określony kąt fazowy i wytworzone w jednym generatorze zwanym generatorem trójfazowym.

Poszczególne obwody generatora trójfazowego nazywać będziemy fazami i oznaczać literami A, B, C lub kolejnymi cyframi 1, 2, 3. Historycznie używano oznaczeń R, S, T lub U, V, W. Obecnie Polska Norma zaleca używanie symboli L1, L2, L3 lub cyfr 1, 2, 3.

Punkt wspólny wszystkich trzech faz generatora oznaczony jest cyfrą 0. Przykładowy układ faz obwodu trójfazowego przedstawia rysunek 1.

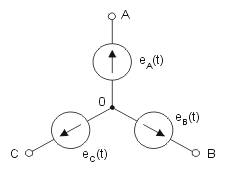
Układ napięć źródłowych generatora trójfazowego nazywać będziemy symetrycznym, jeśli napięcia kolejnych faz są przesunięte względem siebie o kąt 120^o ([latex]\frac{2}{3} \pi[/latex]), a amplitudy ich są sobie równe. Wartości chwilowe poszczególnych napięć fazowych układu symetrycznego można zapisać w postaci:

[latex]e_{A}( t) =| E_{m}| sin( \omega t+\psi )[/latex]

[latex]e_{B}( t) =| E_{m}| sin\left( \omega t+\psi -120^{o}\right)[/latex]

[latex]e_{C}( t) =| E_{m}| sin\left( \omega t+\psi +120^{o}\right)[/latex]

Gdzie E_m oznacza amplitudę, pulsację wspólną dla wszystkich faz a kąt ψ jest początkowym kątem fazowym napięcia w fazie A. W normalnym systemie trójfazowym przyjmuje się tzw. kolejność wirowania zgodną, w której faza B opóźnia się względem fazy A o kąt 120^o, a faza C (opóźniona względem fazy B o kolejny kąt 120^o) wyprzedza fazę A o kąt równy 120^o.

Kąt początkowy Ψ można przyjąć dowolnie, w większości przypadków wygodnie jest przyjąć 0^o lub 90o.

Zarówno generator jak i odbiornik trójfazowy mogą być połączone w topologii gwiazdy lub trójkąta. Przy połączeniu generatora w trójkąt odbiornik jest zasilany napięciem międzyfazowym trójprzewodowym. Przy połączeniu generatora w gwiazdę napięcie zasilające jest napięciem fazowym a liczba przewodów może być równa trzy bądź cztery (przy czterech przewodach zasilających jednym z nich jest przewód zerowy, zwany również przewodem neutralnym).
W układzie trójfazowym odbiornik zawiera również trzy fazy, przy czym może być on połączony w gwiazdę bez przewodu neutralnego (rysunek 2), gwiazdę z przewodem neutralnym (rysunek 3) lub w trójkąt.

Układ bez przewodu neutralnego, a więc trójprzewodowy (Z_N=[latex]\infty[/latex])

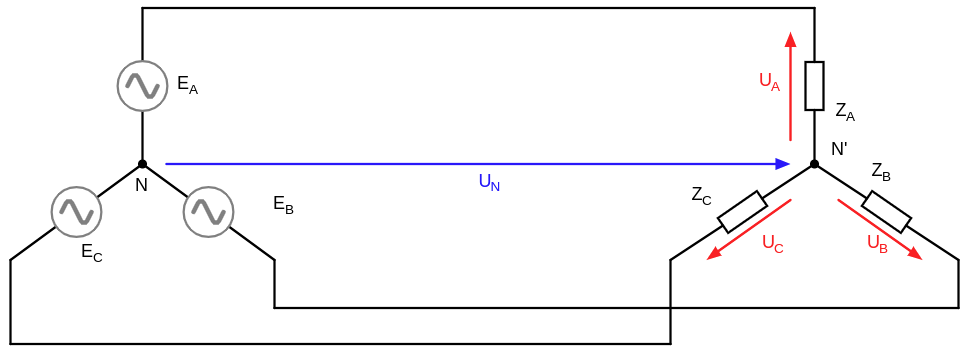
Różnice potencjałów pomiędzy punktem neutralnym źródła i odbiornika, można obliczyć ze wzoru:

[latex]U_{N} =\frac{Y_{A} E_{A} +Y_{B} E_{B} +Y_{C} E_{C}}{Y_{A} +Y_{B} +Y_{C}}[/latex]

Stąd napięcia na elementach odbiornika

[latex]U_{A} =E_{A} -U_{N}[/latex]

[latex]U_{B} =E_{B} -U_{N}[/latex]

[latex]U_{C} =E_{C} -U_{N}[/latex]

zespolone prądy fazowe

[latex]I_{A} =\frac{U_{A}}{Z_{A}}[/latex]

[latex]I_{B} =\frac{U_{B}}{Z_{B}}[/latex]

[latex]I_{C} =\frac{U_{C}}{Z_{C}}[/latex]

ich suma równa jest zeru:

[latex]I_{A} +I_{B} +I_{C} =0[/latex]

Analiza układu trójfazowego połączonego gwiazda-gwiazda z przewodem neutralnym.

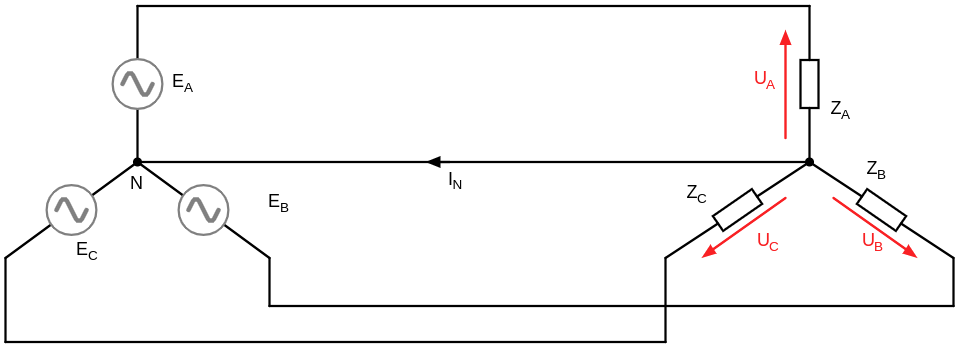
Napięcia na elementach odbiornika są równe napięciom generatora i wynoszą:

[latex]U_{A} =E_{A}[/latex]

[latex]U_{B} =E_{B}[/latex]

[latex]U_{C} =E_{C}[/latex]

stąd zespolone prądy fazowe

[latex]I_{A} =\frac{U_{A}}{Z_{A}}[/latex]

[latex]I_{B} =\frac{U_{B}}{Z_{B}}[/latex]

[latex]I_{C} =\frac{U_{C}}{Z_{C}}[/latex]

Prąd w przewodzie neutralnym jest sumą zespolonych prądów fazowych i wynosi:

[latex]I_{N} =I_{A} +I_{B} +I_{C}[/latex]