Stany nieustalone w obwodzie RC, RL i RLC
Wprowadzenie Teoretyczne
Radosław Roszczyk and Krzysztof Siwek
W wyniku przełączeń, zmiany konfiguracji obwodu lub zmiany wartości parametrów obwodu RLC powstaje w nim stan nieustalony, charakteryzujący się tym, że kształt odpowiedzi obwodu jest inny niż wymuszenia. Po pewnym czasie odpowiedzi tego typu zanikają i ich charakter znów odpowiada charakterowi wymuszenia. Powstaje więc nowy stan ustalony w obwodzie o zmienionej strukturze na skutek przełączenia.
Równania stanu opisujące obwód są zbiorem wielu równań różniczkowych pierwszego rzędu zapisanych w postaci równań macierzowych. Pierwsze macierzowe równanie stanu:
[latex]\frac{dx}{dt} =Ax+Bu[/latex]
opisuje dynamikę obwodu.
Drugie równanie stanu:
[latex]y=Cx+Du[/latex]
definiuje zmienne stanu x(t). Znajomość zmiennych stanu, przy znanych przyszłych wymuszeniach u(t) oraz znanym warunku początkowym x(0) pozwala na obliczenie dowolnej wielkości w obwodzie.
W obwodach elektrycznych zmiennymi stanu tworzącymi wektor x są napięcia wszystkich kondensatorów i prądy wszystkich cewek, dla których obowiązują tak zwane prawa komutacji, pozwalające na wyznaczenie warunków początkowych w obwodzie x(0).
W przypadku istnienia oczek składających się z idealnych wymuszeń napięciowych i kondensatorów lub rozcięć składających się z idealnych wymuszeń prądowych i cewek liczba zmiennych stanu jest mniejsza od liczby elementów reaktancyjnych (kondensatorów i cewek). W przypadku istnienia jeszcze źródeł starowanych w obwodzie ta liczba może ulec dalszej redukcji.
W obwodach elektrycznych proces komutacji modeluje się zwykle przy pomocy wyłączników i przełączników wskazujących na rodzaj przełączenia.
Wyznaczanie stałej czasowej
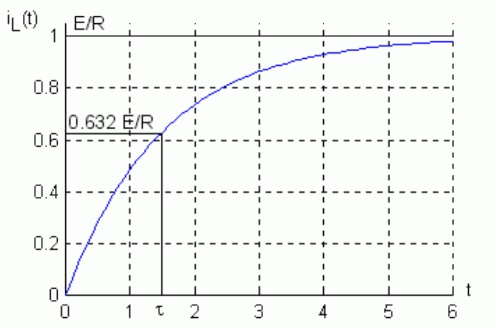
Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Sposób wyznaczenia stałej czasowej został zilustrowany na rysunku 1.
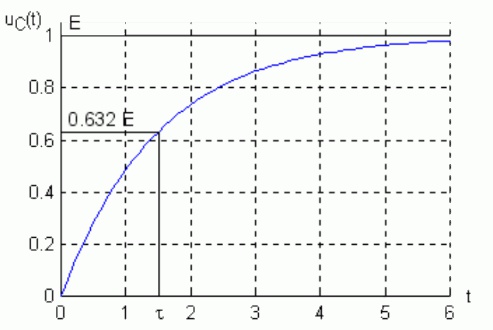
Analogicznie możemy wyznaczyć stałą czasową dla obwodu RC. Różnica będzie polegała na obserwacji przebiegu napięcia w funkcji czasu. Sposób wyznaczenia stałej czasowej dla obwodu RC został zilustrowany na rysunku 2.
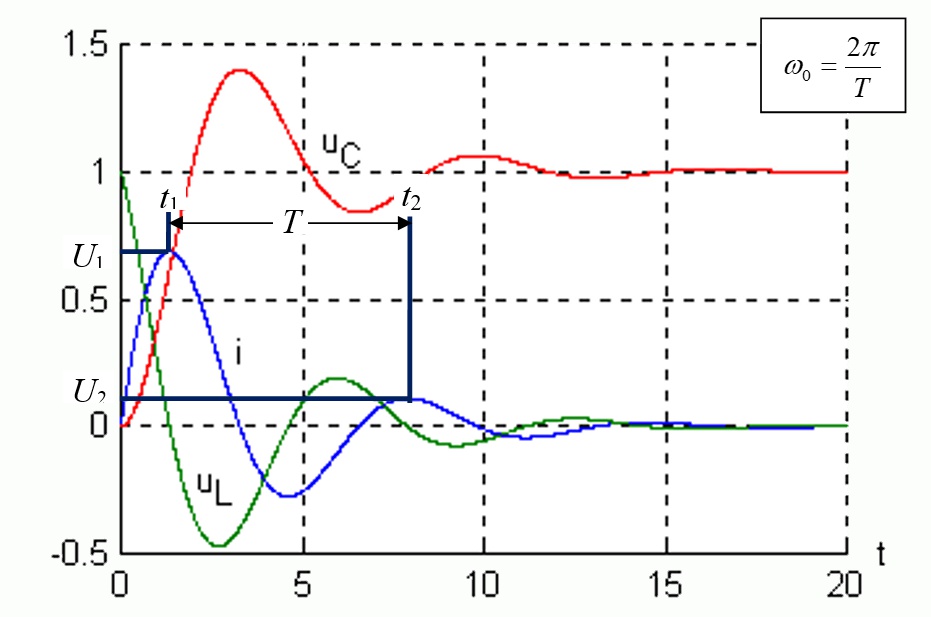
Dla określenia częstotliwości drgań własnych w obwodzie RLC dla przypadku oscylacyjnego należy wyznaczyć chwile czasowe dwóch kolejnych punktów na wykresie odległych od siebie o okres częstotliwości drgań własnych np. przejścia przez zero bądź ekstremów przebiegu: maksimów lub minimów. Na rysunku 3 przedstawiono pomiar okresu dla dwóch kolejnych maksimów.