Wprowadzenie teoretyczne

Rezystor

Rezystor liniowy o rezystancji R jest dwójnikiem pasywnym rozpraszającym energię.

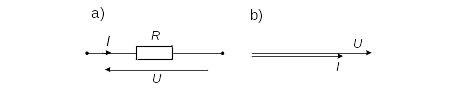
Dla rezystora liniowego rezystancja, prąd i napięcie związane są prawem Ohma

[latex]u=Ri[/latex]

Moc chwilowa pobierana przez rezystor

[latex]p=ui=Ri^{2} =Gu^{2}[/latex]

jest zawsze nieujemna.

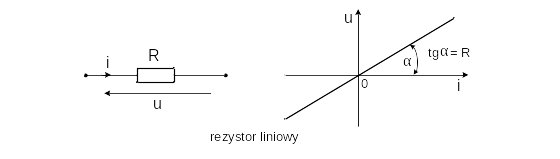
Jeżeli przez rezystor przepływa prąd sinusoidalnie zmienny to ten prąd i napięcie na zaciskach rezystora są sinusoidalne o tej samej pulsacji ω i mają ten sam kąt fazowy φ. Zależności zostały zamieszczone na rysunku 2.

Kondensator

Rezystor liniowy o pojemności C jest dwójnikiem pasywnym. Rysunek 3 przedstawia symbol graficzny kondensatora.

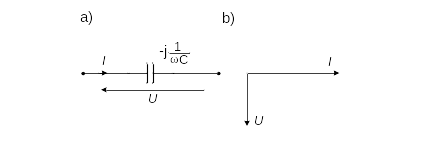
Dla kondensatora liniowego równanie wiążące napięcie i prąd z ładunkiem q

[latex]q=Cu[/latex]

[latex]i=\frac{dq}{dt} =C\frac{du}{dt}[/latex]

Moc chwilowa pobierana przez kondensator

[latex]p=ui=Cu\frac{du}{dt}[/latex]

Energia pobrana przez kondensator w przedziale [latex]( t_{1} ,t_{2})[/latex].

[latex]W( t) =C\int\limits _{t_{1}}^{t_{2}} u( \tau )\frac{du( \tau )}{d\tau } d\tau =\frac{1}{C}\left[ u^{2}( t_{2}) -u^{2}( t_{1})\right][/latex]

Załóżmy, że czas t₁ jest taką chwilą, w której napięcie u(t) jest zerowe. W takim razie wzór na energię upraszcza się do postaci

[latex]W( t_{0} ,t) \ =C\int\limits _{0}^{u( t)} udu=\frac{1}{2} Cu^{2}( t)[/latex]

Zasadniczą cechą kondensatora idealnego jest jego bezstratność, co oznacza, że energia zgromadzona na nim pozostaje w nim zmagazynowana. Zatem kondensator naładowany do napięcia stałego U posiada energię równą

[latex]W=\frac{1}{2}\mathcal{C} U^{2}[/latex]

Kondensator nie pobiera mocy czynnej, może gromadzić energie, jest więc elementem inercyjnym – rysunek 4.

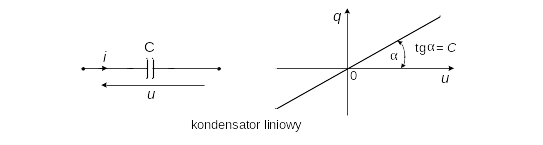
Napięcie kondensatora opóźnia się względem prądu o kąt 90^o.

Cewka

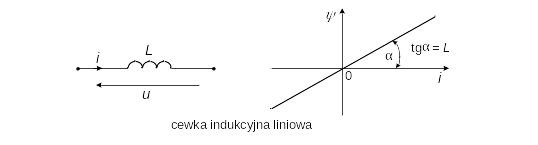
Dla cewki liniowej, prąd i napięcie powiązane są ze skojarzonym strumieniem magnetycznym ψ

[latex]\psi =Li[/latex]

[latex]u=\frac{d\psi }{dt} =L\frac{di}{dt}[/latex]

Moc chwilowa pobierana przez cewkę

[latex]p=ui=Li\frac{di}{dt}[/latex]

Energia pobrana przez cewkę w przedziale [latex]( t_{1} ,t_{2})[/latex]

[latex]p( t) =L\int\limits _{t_{1}}^{t_{2}} i( \tau )\frac{di( \tau )}{i\tau } d\tau =\frac{1}{2} L\left[ i^{2}( t_{2}) -i^{2}( 1_{1})\right][/latex]

Załóżmy, że czas t₁ jest taką chwilą, w której prąd cewki i(t) jest zerowy. W takim razie wzór na energię upraszcza się do postaci

[latex]W( t_{0} ,t) =L\int\limits _{0}^{i( t)} idi=\frac{1}{2} Li^{2}( t)[/latex]

Zasadniczą cechą cewki idealnej jest jej bezstratność, co oznacza, że energia dostarczona do niej pozostaje w niej zmagazynowana. Zatem cewka, przez która przepływa prąd stały I posiada energię równą

[latex]W=\frac{1}{2} LI^{2}[/latex]

Cewka nie pobiera mocy czynnej, może gromadzić energie, jest więc elementem inercyjnym.

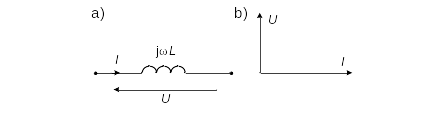
Prąd cewki opóźnia się względem napięcia o kąt 90^o