Instrukcje do ćwiczeń
3. Badanie własności materiałów ferromagnetycznych
1. Wprowadzenie
W każdym atomie znanych nam materiałów występują elektrony krążące po eliptycznych orbitach. Można więc powiedzieć, że następuje przemieszczanie ładunku q=e w czasie obiegu elektronu wokół jądra atomowego. Dodatkowo każdy elektron obraca się wokół własnej osi, co nosi nazwę spinu. Oba te zjawiska powodują pojawienie się magnetycznych momentów orbitalnego i spinowego. Momenty te sumują się wektorowo i ostatecznie każdy atom posiada moment magnetyczny. Może on być różny od zera lub równy zeru. Zewnętrzne pole magnetyczne zakłóca ruch elektronów i pojawia się indukowany moment magnetyczny skierowany zawsze przeciwnie do wektora natężenia pola magnetycznego. Zjawisko powyższe nosi nazwę efektu diamagnetycznego i występuje we wszystkich ośrodkach materialnych i nie zależy od temperatury. Ponieważ wartość momentu indukowanego jest niewielka ujawnia się on tylko w materiałach, dla których wypadkowy moment magnetyczny jest bliski zeru materiały spełniające ten warunek są diamagnetykami.
Jeżeli zaczniemy analizować materiały, których wypadkowy moment magnetyczny jest różny od zera to zaobserwujemy, że ich zachowanie jest zależne od odległości między atomami i rozłożenia elektronów na poszczególnych orbitach. Cechą charakterystyczną jest stosunek [latex]\frac{a}{r}[/latex]
a – odległość atomów,
r – promień orbity niecałkowicie zapełnionej elektronami.
Jeżeli stosunek ten > 6,2 to wzajemne ustawienie momentów magnetycznych jest chaotyczne, za co odpowiadają ruchy cieplne, a ciało jest praktycznie obojętne na działające pole magnetyczne. Ciała wykazujące [latex]\frac{a}{r} > 6,2[/latex] nazywamy paramagnetykami.
Dla materiałów w których [latex]3,2 \leq \frac{a}{r} \leq 6,2[/latex] na skutek oddziaływań międzyatomowych powstają siły wymiany porządkujące ustawienie się sąsiednich dipoli magnetycznych. Gdy do takiego materiału przyłożymy zewnętrzne pole magnetyczne to wszystkie dipole ustawią się równolegle do linii pola zewnętrznego. Efekt ten nazywamy ferromagnetycznym, a materiały takie ferromagnetykami.
Wartość stosunku [latex]\frac{a}{r}[/latex] jest zależna nie tylko od budowy atomowej danego materiału, ale również od temperatury. Wraz ze wzrostem temperatury wzrastają bowiem odległości pomiędzy atomami i w pewnej temperaturze efekt ferromagnetyczny przestaje występować. Temperatura ta jest charakterystyczna i różna dla każdego materiału i nosi nazwę – temperatury Curie.
2. Ferromagnetyki i pętla histerezy
Gdy nie ma zewnętrznego pola magnetycznego dipole magnetyczne ustawiają się w jednym kierunku w ramach makroskopowych domen magnetycznych, których wzajemne ustawienie jest chaotyczne. Pod wpływem pola magnetycznego obszary te ustawiają się wzdłuż linii sił pola magnetycznego i dalsze zwiększanie natężenia pola nie powoduje już zmian ich położenia.
Materiały ferromagnetyczne charakteryzują się zjawiskiem histerezy, które obrazuje nieodwracalne zmiany indukcji magnetycznej w następstwie zmian natężenia zewnętrznego pola magnetycznego. Ich graficznym obrazem jest pętla histerezy obrazująca zmiany B=f(H).
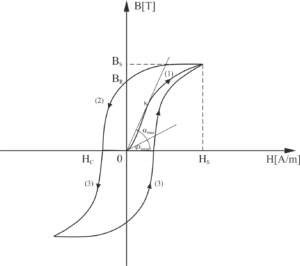 Na rysunku obrazującym pętlę histerezy możemy wyróżnić następujące cykle magnesowania:
Na rysunku obrazującym pętlę histerezy możemy wyróżnić następujące cykle magnesowania:
- Charakterystyka pierwotnego magnesowania;
- Krzywa odmagnesowania;
- Pełna pętla histerezy magnetycznej.
Charakterystyka pierwotnego magnesowania jest to krzywa powstająca przy pierwszym magnesowaniu danego materiału biegnąca od punktu (0;0) do punktu (HS;BS).
BS – indukcja nasycenia, jest największą możliwą do uzyskania w materiale indukcją. Dalsze zwiększanie natężenia pola H nie zwiększa indukcji.
HS – natężenie nasycenia jest natężeniem pola magnetycznego, dla którego występuje indukcja nasycenia.
Krzywa odmagnesowania jest to krzywa powstająca przy zaniku zewnętrznego pola magnetycznego biegnąca od punktu (HS;BS), aż do punktu (HC;0) poprzez punkt (0; BR).
HC – natężenie koercji (natężenie powściągające) jest natężeniem pola magnetycznego przy którym indukcja jest równa zeru.
BR – remanencja (pozostałość magnetyczna) jest indukcją szczątkową materiału namagnesowanego do stanu nasycenia, a następnie odmagnesowanego poprzez zmniejszenie pola zewnętrznego.
Pełna pętla histerezy magnetycznej przedstawia pełny cykl przemagnesowania magnetyka i nosi nazwę granicznej pętli histerezy magnetycznej.
Procesowi przemagnesowywania towarzyszą ustalone straty energii wydzielające się w postaci ciepła. Straty powyższe, zwane stratami na histerezę są proporcjonalne do pola powierzchni odpowiedniej pętli histerezy oraz do częstotliwości prądu magnesującego. Straty energii powodowane są również przez prądy wirowe indukowane w rdzeniu przez okresowo zmienny strumień magnetyczny. Sumę jednostkowych start mocy zużywanej na histerezę i prądy wirowe nazywamy stratnością magnetyczną.
3. Przenikalność magnetyczna μ
Każdy materiał możemy scharakteryzować pod względem jego oddziaływania z zewnętrznym polem magnetycznym. Jak wspomniano we wprowadzeniu, własności magnetyczne są wynikiem zjawisk kwantowo mechanicznych. Jednak do opisu materiałów w świecie makroskopowym wygodniej jest używać pojęcia przenikalności magnetycznej.
μ – przenikalność magnetyczna materiału informuje nas o ile razy zmieni się pole magnetyczne po przejściu przez materiał.
[latex]\mu =\mu_{r} \mu_{0} \left [ \frac{H}{m} \right ][/latex]
μ0 – przenikalność magnetyczna próżni określona jest na poziomie [latex]4\cdot 10^{-7} \left [ \frac{H}{m} \right ][/latex]
μr – przenikalność względna materiału informuje ile razy przenikalność materiału jest większa od przenikalności magnetycznej próżni.
Dla materiałów para- i diamagnetycznych indukcja pola magnetycznego i natężenie tego pola są związane zależnością B = μ·H. W materiałach ferromagnetycznych zależność pomiędzy B i H jest nieliniowa i określona krzywą magnesowania. Jedynie w konkretnym punkcie możemy powiedzieć, że zależność B = μ·H, jest nadal spełniona.
W odniesieniu do ferromagnetyków najczęściej jest używane pojęcie przenikalności magnetycznej normalnej związanej z pierwotną krzywą magnesowania. Ponieważ przenikalność magnetyczna normalna wyraża się zależnością μ = B/H jest więc proporcjonalna do tangensa kąta a zawartego pomiędzy osią odciętych i prostą przechodzącą przez dany punkt krzywej pierwotnego magnesowania czyli μ = B/H = k tgα. Wynika stąd, że przenikalność wzrasta od pewnej wartości początkowej μpocz (odpowiadającej kątowi αpocz), do pewnej wartości maksymalnej μmax (odpowiadającej kątowi αmax w punkcie k krzywej), po czym znowu maleje.
4. Krzywa pierwotnego magnesowania (krzywa komutacyjna)
Krzywą pierwotnego magnesowania możemy otrzymać poprzez powolne namagnesowanie próbki polem stałym lub wolnozmiennym. Wygodniej jednak, ze względów pomiarowych, jest posłużyć się krzywą komutacyjną. Otrzymujemy ją łącząc wierzchołki pętli histerezy dla kolejnych wartości prądu magnesującego aż do osiągnięcia stanu nasycenia.
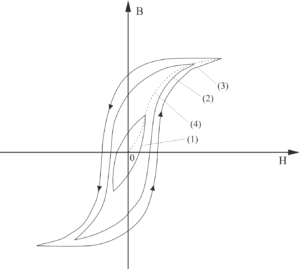
4 – krzywa komutacyjna
4. Podstawowe parametry materiałów magnetycznych
Materiały magnetyczne dzielą się na dwie zasadnicze grupy:
- materiały magnetycznie miękkie,
- materiały magnetycznie twarde.
Cechą wyróżniającą obydwie grupy materiałów jest szerokość granicznej pętli histerezy.
Materiały magnetycznie miękkie odznaczają się bardzo wąską graniczną pętlą histerezy. Natężenie powściągające Hc nie przekracza w tym przypadku wartości 200 A/m, a może być nawet mniejsze od 1 A/m. Materiały magnetycznie miękkie łatwo się magnesują i łatwo się odmagnesowują. Histereza powoduje tu minimalne straty energii. Z tych powodów materiały te są stosowane na rdzenie elektromagnesów prądu stałego oraz wszelkie obwody magnetyczne pracujące przy okresowo zmiennych strumieniach magnetycznych (maszyny elektryczne, transformatory, elektromagnesy prądu zmiennego, dławiki itp.). Do materiałów magnetycznie miękkich należą: żelazo, stopy żelaza z krzemem (stale krzemowe), stopy żelaza z niklem (permaloje), żelaza z kobaltem (permedury), żelaza z aluminium oraz ferryty (spieki tlenków metali). Cechą charakterystyczną ferrytów jest bardzo wysoka rezystywność. W celu skutecznego ograniczenia strat na prądy wirowe w urządzeniach wielkiej częstotliwości są stosowane tzw. rdzenie proszkowe, wykonane z drobno sproszkowanego magnetyka spojonego utwardzoną żywicą.
Materiały magnetycznie twarde mają bardzo szeroką graniczną pętlą histerezy. Wartość Hc jest w tym przypadku nie mniejsza od 4000 A/m, a niekiedy jest większa nawet od 200 000 A/m. Materiały magnetycznie twarde po namagnesowaniu do nasycenia zachowują w sposób trwały uzyskane własności magnetyczne. Z tego względu są one używane do wytwarzania wszelkiego rodzaju magnesów trwałych. Do materiałów magnetycznie twardych należą stale węglowe i stopowe zawierające chrom, wolfram, kobalt, molibden, stopy żelazo-aluminium-nikiel (Alni), stopy żelazo-aluminium-nikiel-kobalt (Alnico)
Własności materiałów magnetycznych charakteryzują wspomniane wyżej parametry, a w szczególności:
- Komutacyjna krzywa magnesowania, tzn. krzywa przechodząca przez wierzchołki kolejnych pętli histerezy. Jest ona zbliżona do krzywej pierwotnego magnesowania,
- Remanencja BR [T],
- Koercja HC[latex]\left [ \frac{A}{m} \right ][/latex],
- Przenikalność magnetyczna początkowa μpocz [latex]\left [ \frac{H}{m} \right ][/latex] oraz maksymalna μmax [latex]\left [ \frac{H}{m} \right ][/latex],
- Indukcja nasycenia BS [T],
- Maksymalne natężenie pola magnetycznego HS [latex]\left [ \frac{A}{m} \right ][/latex],
- Maksymalna wartość iloczynu BS·HS, co jest miarą energii zgromadzonej w magnesie BHmax [latex]\left [ \frac{W}{m^3} \right ][/latex].
5. Metody badań materiałów magnetycznych
Badania materiałów magnetycznych możemy przeprowadzać przy polach stałych jako statyczne oraz przy polach zmiennych jako dynamiczne, co ostatecznie powoduje podział metod badawczych na:
- badanie materiałów magnetycznie miękkich w stałych polach magnetycznych,
- badanie materiałów magnetycznie miękkich w przemiennych polach magnetycznych,
- badanie materiałów magnetycznie twardych.
Próbka magnetyczna tworzy część lub całość obwodu magnetycznego. Pole magnetyczne jest uzyskiwane za pomocą cewek z prądem. W zależności od kształtu próbki i obwodu magnetycznego wyróżniamy:
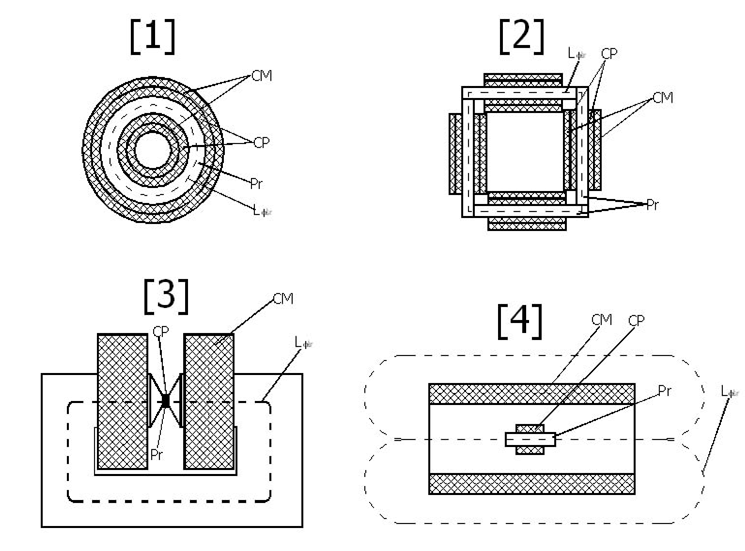
- Układy do badania próbek zamkniętych pierścieniowych [1] i ramowych [2]. Obwód magnetyczny jest tu pierścieniem zwiniętym z blachy z nawiniętymi uzwojeniami lub pakietem blach, który wsuwa się do zestawu stałych cewek. Jest to tzw. aparat Epsteina.
- Układy do badania próbek w zamkniętych obwodach, gdzie próbka stanowi tylko część obwodu magnetycznego tzw. permeatry jarzmowe [3]. Próbka zamyka obwód magnetyczny jarzma, na którym nawinięte są stałe uzwojenia magnesujące i pomiarowe.
- Układy do badania próbek otwartych [4] gdzie prostą próbkę wkładamy do długiej cewki magnesującej.
Wadą układów otwartych jest mniejsza dokładność rekompensowana prostotą układu (stałe cewki magnesujące) oraz szybkością pomiaru i możliwością wykonywania pomiarów seryjnych. Badanie próbek pierścieniowych jest bardziej dokładne jednak przez konieczność wykonania uzwojeń na zamkniętym obwodzie magnetycznym jest długotrwałe. Pomiar indukcji magnetycznej B jest możliwy za pomocą pomiaru indukcji w szczelinie pośrednio (z prądu magnesującego cewki po odpowiednim przekształceniu) lub bezpośrednio np. za pomocą czujników hallotronowych. Pomiar natężenia pola H jest możliwy za pomocą pomiaru prądu magnesującego. Poniżej przedstawiono przykładowe układy próbek do badań.
 7. Układ pomiarowy i opis metody pomiarowej
7. Układ pomiarowy i opis metody pomiarowej
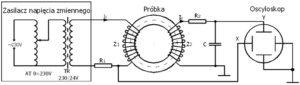
Do wyznaczenia pętli histerezy oraz krzywej komutacyjnej posłużymy się próbkami pierścieniowymi wyposażonymi w uzwojenia oraz kilka prostych elementów dyskretnych. Układ zasilany jest z układu autotransformatora oraz transformatora obniżającego napięcie do 48 V. Na ekranie oscyloskopu otrzymujemy obraz pętli histerezy. Znając wartości elementów dyskretnych możemy przeliczyć wartości napięć w odpowiednich punktach obrazu na wartości B lub H. Zasada pomiaru jest następująca: w obwodzie pierwotnym (N1) pod wpływem napięcia płynie zmienny prąd I1 wytwarzając w rdzeniu ferromagnetycznym zmienne pole magnetyczne o natężeniu proporcjonalnym do tego prądu. Na oporniku R1 powstaje spadek napięcia UR1 proporcjonalny do prądu I1, który podawany jest na płytki odchylania poziomego X oscyloskopu (pełni rolę tzw. podstawy czasu dla oscyloskopu). Z prawa Ampera wiemy, że [latex]\oint \overrightarrow{H}\cdot \overrightarrow{dl}=i[/latex], całka z wektora natężenia pola magnetycznego po obwodzie zamkniętym jest równa sumie prądów przepływających przez kontur całkowania [latex]\overrightarrow{H}\cdot \overrightarrow{dl}=Hdl[/latex]. Jeżeli konturem całkowania jest okrąg o promieniu r leżący wewnątrz próbki to [latex]\oint Hdl=2\pi r H=N_{1}\cdot I_{1}[/latex], a zatem dla cewki toroidalnej przyjmiemy wartość r = rśr, gdzie [latex]r_{śr}=\frac{b+a}{2}[/latex].
W efekcie końcowym otrzymujemy wyrażenie wiążące napięcie na oporniku R1 z natężeniem pola magnetycznego H.
[latex]H=\frac{N_{1}}{2\pi r_{śr}}I_{1}=\frac{N_{1}}{2\pi r_{śr}}\cdot \frac{U_{R1}}{R_{1}}=\frac{N_{1}}{2 R_{1}\pi r_{śr}}U_{R1}[/latex]
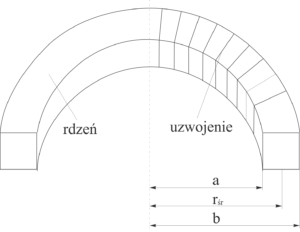 Rysunek przedstawia geometrię próbki i usytuowanie rśr.
Rysunek przedstawia geometrię próbki i usytuowanie rśr.
Zmienny strumień magnetyczny wytwarza w uzwojeniu wtórnym (N2) SEM indukcji. Ta siła elektromotoryczna jest zgodnie z prawem indukcji równa [latex]E=-N_{2}\cdot \frac{d\phi }{dt}[/latex].
Oznaczamy przez [latex]\overrightarrow{dn}[/latex] jednostkowy wektor normalny do powierzchni S obejmowanej przez zwój cewki otrzymujemy [latex]\varphi= \overrightarrow{B} \cdot \overrightarrow{dn}\cdot S[/latex]. Ponieważ w przypadku cewki toroidalnej wektory [latex]\overrightarrow{B}[/latex] oraz [latex]\overrightarrow{dn}[/latex] są równoległe to otrzymujemy [latex]E=-N_{2}\cdot S \cdot \frac{dB}{dt}[/latex]. Napięcie na uzwojeniu wtórnym (N2) jest proporcjonalne do pochodnej indukcji. Jeżeli chcemy obejrzeć i zmierzyć pętlę histerezy to na płytki odchylania oscyloskopu musimy podać napięcie proporcjonalne do B. Aby tego dokonać zastosujemy prosty układ całkujący RC gdzie:
[latex]U_C=\frac{1}{RC}\int E d t=-\frac{1}{RC}\cdot N_2\cdot S\cdot B,[/latex]
co po przekształceniu pozwala otrzymać zależność pomiędzy B a napięciem UC doprowadzonym do płytek odchylania pionowego Y.
[latex]B=\frac{R_2\cdot C}{N_2\cdot S}\cdot U_C[/latex]
Wartości napięć UR1 oraz UC są wartościami maksymalnymi i odczytujemy je bezpośrednio z oscyloskopu.
8. Sposób przeprowadzenia pomiarów i opracowanie wyników
Wymiary Próbki, jej przekrój, oraz wartości R1, R2, C są podane na tabliczce przy każdym rdzeniu ferromagnetycznym. Układ należy podłączyć do zasilania oraz podłączyć oscyloskop do odpowiednich gniazd pomiarowych typu BNC. Ustawić oscyloskop w tryb pracy XY. Regulując autotransformatorem zwiększać napięcie zasilające i obserwować pętle histerezy. Notować kolejne punkty konieczne do wyznaczenia krzywej komutacyjnej. Po osiągnięciu maksymalnej pętli histerezy przenieść jej obraz do protokołu. Otrzymane napięcia posłużą do obliczenia B i H. Otrzymane wyniki zanotować w tabeli, przeprowadzić obliczenia i wyciągnąć wnioski.
Przykładowe tabele pomiarowe
Pomiar Bs i Hs
| Lp. | [latex]U_{R1}\ [V][/latex] | [latex]H_S\ \left [ \frac{A}{m} \right ][/latex] | [latex]U_{C}\ [V][/latex] | [latex]B_{S}\ [T][/latex] |
| 1 | ||||
| 2 |
Pomiar Br i Hc
| Lp. | [latex]U_{R1}\ [V][/latex] | [latex]H_c\ \left [ \frac{A}{m} \right ][/latex] | [latex]U_{C}\ [V][/latex] | [latex]B_{r}\ [T][/latex] |
| 1 | ||||
| 2 |
Parametry materiałów magnetycznie miękkich
| Materiał | Zawartość składników [%] (reszta żelazo) |
µr pocz | µr max | Hc [A/m] |
Bs [T] |
| Żelazo przetopione w wodorze |
0,005 C; 0,001 O2 | 20 000 | 340 000 | 2,4 | 2,15 |
| Żelazo elektrolityczne | 0,02 C; 0,01 O2 | 3 300 | 21 500 | 6,4 | 2,17 |
| Stal niskowęglowa | 0,02 C; 0,035 O2 | 2 000 | 144,0 | 2,10 | |
| Stal krzemowa izotropowa | 4,05 Si; 0,015 C | 7 000 | 40,0 | 1,97 | |
| Stal krzemowa izotropowa | 3,0 Si | 30 000 | 12,0 | 2,00 | |
| Monokrystaliczny stop | 3 Si | 3 800 000 | |||
| Hyperm 50 (permaloj) | 50 Ni | 3 350 | 28 000 | 4,8 | 1,50 |
| Permaloj C | 78 Ni | 25 000 | 120 000 | 2,4 | 0,80 |
| Supermalloy | 79 Ni; 5,0 Mo; 0,3 Mn | 800 000 | 0,2 | 0,80 | |
| Finmet | 1 Cu; 3 Nb; 13,5 Si; 9 B | 100 000 | < 1,0 | 1,25 | |
| Alsifer (rdzenie proszkowe) | 5,6 Al; 9,5 Si | 35 000 | 120 000 | 1,6 | |
| Ferryt Fe2O3+ZnO+NiO | 250 | 1000 | 110 |
Parametry materiałów magnetycznie twardych
| Materiał | Zawartość składników [%] (reszta żelazo) |
Br [T] |
Hc [A/m] |
BHmax [J/m3] |
| Stal węglowa (zahartowana) | 1 C; 1 Mn | 0,86 | 4 800 | 2 000 |
| Stal wolframowa W6 | 6 W; 0,3 Mn; 0,7 C | 1,00 | 4 950 | 2 300 |
| Alni 110 | 13 Al; 25 Ni; 3 Cu | 0,54 | 45 000 | 10 000 |
| Alnico VI | 8 Al; 15 Ni; 24 Co; 3 Cu; 1 Ti | 1,00 | 60 000 | 35 000 |
| Alnico XII | 6 Al; 18 Ni; 35 Co; 8 Ti | 0,58 | 76 000 | 15 000 |
| Platyno-kobalt | 77 Pt; 23 Co | 0,45 | 208 000 | 38 000 |
| Ferryt kobaltowy | 30 Fe2O3; 44 Fe3O4; 26 Co2O3 | 0,16 | 86 000 | 5 000 |
| Ferryt barowy | BaO × 6Fe2O3 | 0,20 | 120 000 | 4 000 |
| Stop Nd2Fe14B (neodymowy) | 1,30 | do 1 000 000 000 | do 300 000 |
