Per-unit Calculations

In electrical power engineering we deal with many characteristic calculations, eg.:
– Load flow calculations
– Short-circuit calculations
– Stability
– Reliability calculations
– Economic dispatch
– Unit commitment

Analysing of large multi-voltage systems is time consuming, because on each stage of transformation we have to recalculate:
– currents and voltages as a function of transformer ratio t,
– impedances and admittances as a function of square of transformer ratio t².

Majority of practical calculations in electrical power engineering are not carried on in denominate numbers – but in per-unit system. Calculations in this system are simplified because expressed quantities do not change when they are referred from one side of a transformer to the other. This is a significant advantage in power system analysis where large numbers of transformers may be encountered.

Let’s consider such problem. We have a segment of a power system consisting of two single phase lines and a power transformer. We want to convert the values from one side to the other.

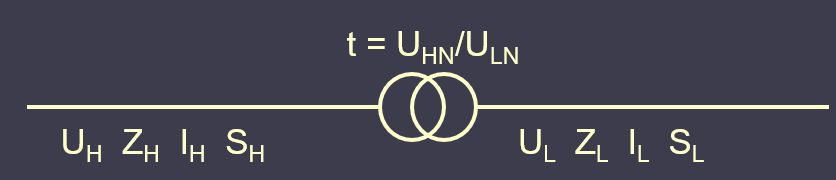
It is a power transformer so, neglecting the losses, we get:
S_H = S_L

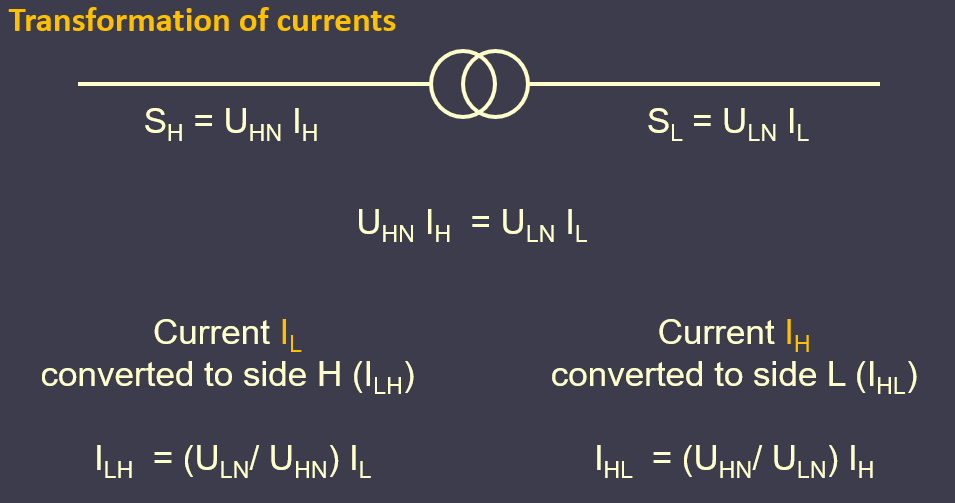
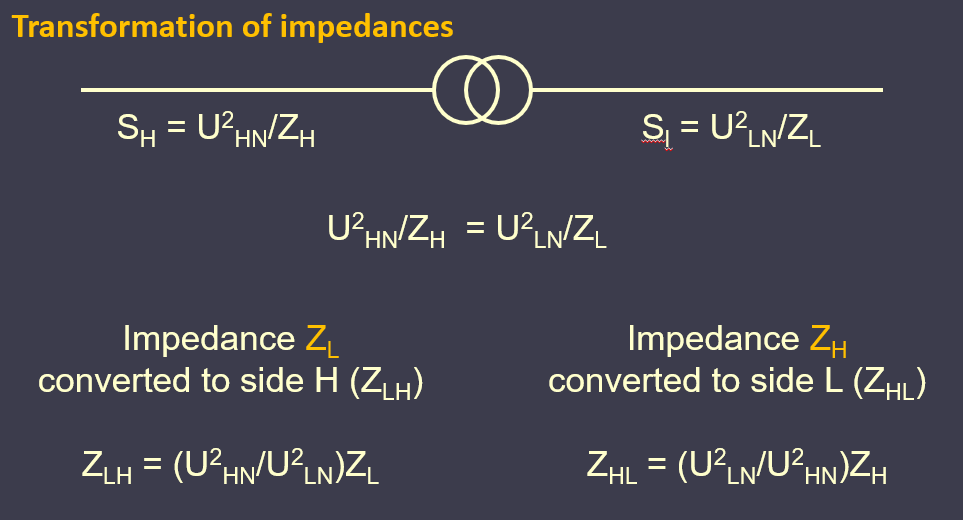
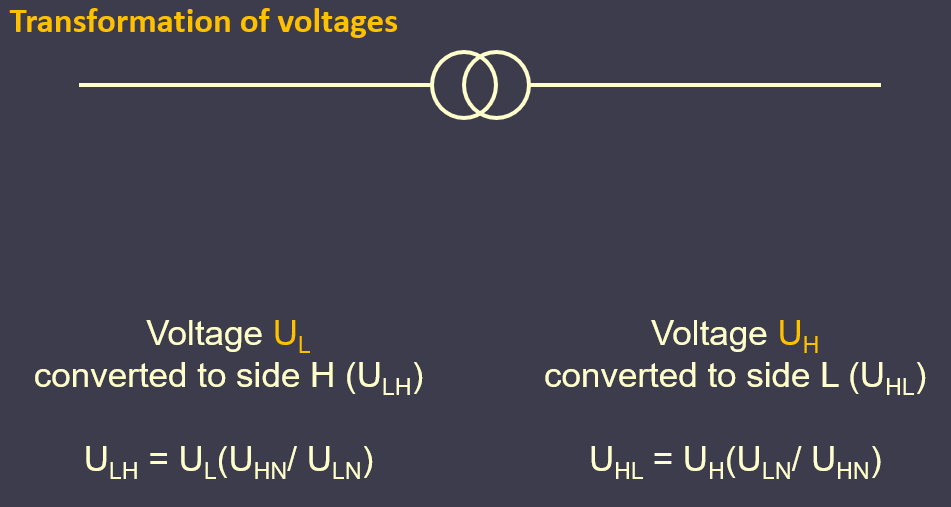
To avoid permanent conversion of values and parameters by transformer ratio we recalculate both parameters and values on relative units, per units, and then we conduct all analytical calculations. Received calculation results are converted back on denominate units according to precisely defined procedure.

Therefore we have three stages of calculations:
– The way of basic units selection
– Conversion from denominate units to per units
– Return from p.u. to denominate units

Principles of basic units selection

The base of calculations in p.u. are basic units, marked with lower
index „b”. These are four following values:
– Basic power S_b (three-phase (3ph) or single phase (1ph)),
– Basic phase current I_b,
– Basic voltage U_b (phase-to-phase (3ph) or phase (1ph)),
– Basic impedance Z_b or admittance Y_b.

They are denominate units and they are scalars.

It is obvious that it is enough to choose arbitrary two of these values because the rest can be calculated from Ohm’s Law and equation for power, using the following formulae
– for single phase system
Z_b = U_b/I_b             S_b = U_bI_b          Yb = 1/Z_b
– for three-phase system
Z_b = U_b/ √3 I_b       S_b = √3 U_bI_b       Y_b = 1/Z_b

Mentioned above arbitrary choice of two values is not so arbitrary in the practice of system calculations. If we neglect power losses then apparent power is unchangeable in the system, independent of voltage level. It forces us to choose basic power Sb as one of the two mentioned basic units.

The second value which should be chosen is basic voltage phase-to-phase (3ph) or phase (1ph) equal to nominal voltage on the given level of transformation U_b = U_N. The question is if one or several voltage levels ought to be chosen.

The choice of basic power and basic voltage enables to determine the rest of basic units:
– for three-phase system

I_b = S_b / √3 U_b     Z_b = U_b / √3 I_b = U_b²/ S_b     Yb = 1 / Z_b = S_b / U_b²

– for single phase system

I_b = S_b / U_b        Z_b = U_b / I_b = U_b² / S_b      Y_b = 1 / Z_b = S_b / U_b²

During calculations we have as many sets of basic units as many voltage levels there are. Having many sets of basic units we must remember that on the given voltage level we use only one set of basic units, corresponding only to that level of voltage. In consequence we get all parameters and variables in undenominational form:

U_pu = U / U_b          I_pu = I / I_b             Y_pu = Y / Y_b

S_pu = S / S_b            Z_pu = Z / Z_b